
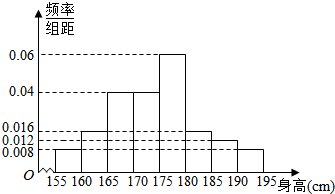
 从某校高二年级800名学生中随机抽取100名测量身高,得到频率分布直方图如图.
从某校高二年级800名学生中随机抽取100名测量身高,得到频率分布直方图如图.分析 (1)根据频率分布直方图,求出身高在170厘米以下的频率,再求对应的频数即可;
(2)根据频率和为1,求出身高在185~190内的频率为,再求平均数.
解答 解:(1)根据频率分布直方图,得;
身高在170厘米以下的频率为
(0.008+0.016+0.04)×5=0.32,
所以这100名学生中身高在170厘米以下的人数为
100×0.32=32;
(2)根据频率分布直方图,
估计这800名学生的平均身高为
$\overline{x}$=157.5×0.008×5+162.5×0.016×5+170×0.04×10
+177.5×0.06×5+182.5×0.016×5+187.5×0.06+192.5×0.008×5
=174.1厘米
点评 本题考查了频率分布直方图的应用问题,也考查了计算平均数的问题,是基础题目.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:填空题
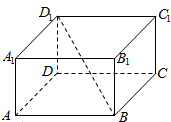 如图,长方体ABCD-A1B1C1D1中,O为BD1的中点,三棱锥O-ABD的体积为V1,四棱锥O-ADD1A1的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值为$\frac{1}{2}$.
如图,长方体ABCD-A1B1C1D1中,O为BD1的中点,三棱锥O-ABD的体积为V1,四棱锥O-ADD1A1的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值为$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com