
【题目】如图所示,正方体ABCD-A1B1C1D1中,M、N分别是A1B1、B1C1的中点,问:

(1)AM和CN是否是异面直线?说明理由;
(2)D1B和CC1是否是异面直线?说明理由.
【答案】(1)不是异面直线(2)是异面直线
【解析】试题分析:(1)根据公理4得MN∥A1C1∥AC,所以两直线共面(2)由异面直线判定定理可得两直线为异面直线
试题解析: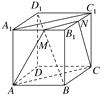
(1)不是异面直线,理由:连结MN,A1C1、AC,如图,因为M、N分别是A1B1、B1C1的中点,所以MN∥A1C1.又因为A1A![]() D1D,D1D
D1D,D1D![]() C1C,所以A1A
C1C,所以A1A![]() C1C,四边形A1ACC1为平行四边形,所以A1C1∥AC,故MN∥A1C1∥AC,所以A、M、N、C在同一个平面内,故AM和CN不是异面直线.
C1C,四边形A1ACC1为平行四边形,所以A1C1∥AC,故MN∥A1C1∥AC,所以A、M、N、C在同一个平面内,故AM和CN不是异面直线.
(2)是异面直线,证明如下:假设D1B与CC1在同一个平面CC1D1内,则B∈平面CC1D1,C∈平面CC1D1,所以BC平面CC1D1,这显然是不正确的,所以假设不成立,故D1B与CC1是异面直线.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】若函数![]() (e=2.71828
(e=2.71828![]() ,是自然对数的底数)在
,是自然对数的底数)在![]() 的定义域上单调递增,则称函数
的定义域上单调递增,则称函数![]() 具有M性质,下列函数中具有M性质的是( )
具有M性质,下列函数中具有M性质的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种药种植基地有两处种植区的药材需在下周一、周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘,由于下雨会影响药材的收益,若基地收益如下表所示:已知下周一和下周二无雨的概率相同且为![]() ,两天是否下雨互不影响,若两天都下雨的概率为
,两天是否下雨互不影响,若两天都下雨的概率为![]()

(1)求![]() 及基地的预期收益;
及基地的预期收益;
(2)若该基地额外聘请工人,可在周一当天完成全部采摘任务,若周一无雨时收益为![]() 万元,有雨时收益为
万元,有雨时收益为![]() 万元,且额外聘请工人的成本为
万元,且额外聘请工人的成本为![]() 元,问该基地是否应该额外聘请工人,请说明理由.
元,问该基地是否应该额外聘请工人,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有![]() 五辆汽车,其中
五辆汽车,其中![]() 两辆汽车的车牌尾号均为1.
两辆汽车的车牌尾号均为1. ![]() 两辆汽车的车牌尾号均为2,
两辆汽车的车牌尾号均为2, ![]() 车的车牌尾号为6,已知在非限行日,每辆车可能出车或不出车,
车的车牌尾号为6,已知在非限行日,每辆车可能出车或不出车, ![]() 三辆汽车每天出车的概率均为
三辆汽车每天出车的概率均为![]() ,
, ![]() 两辆汽车每天出车的概率均为
两辆汽车每天出车的概率均为![]() ,且五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
,且五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
(1)求该公司在星期一至少有2辆汽车出国的概率;
(2)设![]() 表示该公司在星期二和星期三两天出车的车辆数之和,求
表示该公司在星期二和星期三两天出车的车辆数之和,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,
的焦点, ![]() 为抛物线
为抛物线![]() 上不同的两点,
上不同的两点, ![]() 分别是抛物线
分别是抛物线![]() 在点
在点![]() 、点
、点![]() 处的切线,
处的切线, ![]() 是
是![]() 的交点.
的交点.
(1)当直线![]() 经过焦点
经过焦点![]() 时,求证:点
时,求证:点![]() 在定直线上;
在定直线上;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入![]() 的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
8 | 3 | 4 |
1 | 5 | 9 |
6 | 7 | 2 |
A. 9 B. 8 C. 6 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com