
【题目】如图,直三棱柱![]() 中,点
中,点![]() 是棱
是棱![]() 的中点.
的中点.
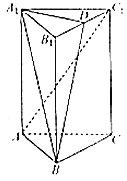
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,
,![]() ,在棱
,在棱![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
科目:高中数学 来源: 题型:
【题目】有甲、乙两家公司都需要招聘求职者,这两家公司的聘用信息如下:
甲公司 | 乙公司 | |||||||||
职位 | A | B | C | D | 职位 | A | B | C | D | |
月薪/元 | 6000 | 7000 | 8000 | 9000 | 月薪/元 | 5000 | 7000 | 9000 | 11000 | |
获得相应职位概率 | 0.4 | 0.3 | 0.2 | 0.1 | 获得相应职位概率 | 0.4 | 0.3 | 0.2 | 0.1 | |
(1)根据以上信息,如果你是该求职者,你会选择哪一家公司?说明理由;
(2)某课外实习作业小组调查了1000名职场人士,就选择这两家公司的意愿做了统计,得到以下数据分布:
选择意愿 人员结构 | 40岁以上(含40岁)男性 | 40岁以上(含40岁)女性 | 40岁以下男性 | 40岁以下女性 |
选择甲公司 | 110 | 120 | 140 | 80 |
选择乙公司 | 150 | 90 | 200 | 110 |
若分析选择意愿与年龄这两个分类变量,计算得到的K2的观测值为k1=5.5513,测得出“选择意愿与年龄有关系”的结论犯错误的概率的上限是多少?并用统计学知识分析,选择意愿与年龄变量和性别变量哪一个关联性更大?
附:![]()
| 0.050 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]() ,
,![]() (
(![]() ),数列
),数列![]() 满足:
满足:![]() ,
,![]() (
(![]() ),数列
),数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求证:数列![]() 是等比数列;
是等比数列;
(3)求证:数列![]() 是递增数列;若当且仅当
是递增数列;若当且仅当![]() 时,
时,![]() 取得最小值,求
取得最小值,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出四个命题:①若x2﹣3x+2=0,则x=1或x=2;②若x=y=0,则x2+y2=0;③已知x,y∈N,若x+y是奇数,则x、y中一个是奇数,一个是偶数;④若x1,x2是方程x2﹣2![]() x+2=0的两根,则x1,x2可以是一椭圆与一双曲线的离心率,那么( )
x+2=0的两根,则x1,x2可以是一椭圆与一双曲线的离心率,那么( )
A.③的否命题为假B.①的逆否命题为假
C.②的逆命题为真D.④的逆否命题为假
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2xlnx+1.
(1)求曲线y=f(x)在点(e,f(e))处的切线方程;
(2)若关于x的不等式f(x)![]() x2+ax在(
x2+ax在(![]() ,+∞)上恒成立,求实数a的取值范围.
,+∞)上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为梯形,![]() ,
,![]() ,
,![]() ,
,![]() 平面ABCD.
平面ABCD.
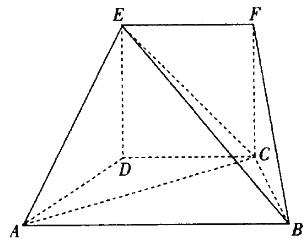
![]() 求BE与平面EAC所成角的正弦值;
求BE与平面EAC所成角的正弦值;
![]() 线段BE上是否存在点M,使平面
线段BE上是否存在点M,使平面![]() 平面DFM?若存在,求
平面DFM?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检验设备M与设备N的生产效率,研究人员作出统计,得到如下表所示的结果,则
设备M | 设备N | |
生产出的合格产品 | 48 | 43 |
生产出的不合格产品 | 2 | 7 |
附:
P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式:![]() ,其中
,其中![]() .
.
A. 有90%的把握认为生产的产品质量与设备的选择有关
B. 没有90%的把握认为生产的产品质量与设备的选择有关
C. 可以在犯错误的概率不超过0.01的前提下认为生产的产品质量与设备的选择有关
D. 不能在犯错误的概率不超过0.1的前提下认为生产的产品质量与设备的选择有关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足x2﹣4ax+3a2<0(a>0),命题q:实数x满足x2﹣5x+6<0.
(1)若a=1,且p∧q为真命题,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物),为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5浓度的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量x(万辆) | 100 | 102 | 108 | 114 | 116 |
PM2.5的浓度y(微克/立方米) | 78 | 80 | 84 | 88 | 90 |
(1)根据上表数据,用最小二乘法,求出y关于x的线性回归方程![]() x
x![]() ;
;
(2)若周六同一时间段车流量200万辆,试根据(1)求出的线性回归方程,预测此时PM2.5的浓度为多少?
(参考公式: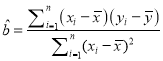 ,
,![]()
![]() ;参考数据:
;参考数据:![]() xi=540,
xi=540,![]() yi=420)
yi=420)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com