
【题目】在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AC=![]() ,AB=2BC=2,AC⊥FB.
,AB=2BC=2,AC⊥FB.

(1)求证:AC⊥平面FBC;
(2)求四面体FBCD的体积;
(3)线段AC上是否存在点M,使得EA∥平面FDM?证明你的结论.
【答案】(1) 见解析.(2) ![]() .(3) 见解析.
.(3) 见解析.
【解析】试题分析:
(1)(2)(3)
试题解析:
(1)证明:在△ABC中,
∵AC=![]() ,AB=2,BC=1,
,AB=2,BC=1,
∴![]() ,
,
∴![]() ,
,
∴AC⊥BC.
又AC⊥FB,BC ∩FB=B,
∴AC⊥平面FBC.
(2)∵AC⊥平面FBC,FC平面FBC,
∴AC⊥FC.
∵CD⊥FC,AC∩CD=C,
∴FC⊥平面ABCD.
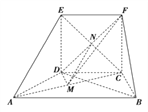
在等腰梯形ABCD中可得∠BCD=120°,CB=DC=1,
∴FC=1.
∴![]() ,
,
∴四面体FBCD的体积为![]() .
.
(3)线段AC上存在点M,且M为AC中点时,有EA∥平面FDM.
证明如下:
连接CE,与DF交于点N,连接MN.
∵四边形CDEF为正方形,
∴N为CE中点.
∴EA∥MN.
又MN平面FDM,EA平面FDM,
∴EA∥平面FDM.
故线段AC上存在点M,使得EA∥平面FDM成立.


科目:高中数学 来源: 题型:
【题目】下列命题错误的是( )
A. 若p∨q为假命题,则p∧q为假命题
B. 若a,b∈[0,1],则不等式a2+b2<![]() 成立的概率是
成立的概率是![]()
C. 命题“x∈R,使得x2+x+1<0”的否定是“x∈R,x2+x+1≥0”
D. 已知函数f(x)可导,则“f′(x0)=0”是“x0是函数f(x)的极值点”的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥PABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直;
②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积;
④直线AE与直线BF是异面直线.
以上结论正确的是________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求f(x)的定义域;
(2)当x∈(1,+∞),
①求证:f(x)在区间(1,+∞)上是减函数;
②求使关系式f(2+m)>f(2m-1)成立的实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ADC=60°,侧面PDC是正三角形,平面PDC⊥平面ABCD,CD=2,M为PB的中点.

(1)求证:PA⊥平面CDM.
(2)求二面角D-MC-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :方程
:方程![]() 有两个不相等的实数根;命题
有两个不相等的实数根;命题![]() :不等式
:不等式![]() 的解集为
的解集为![]() .若
.若![]() 或
或![]() 为真,
为真,![]() 为假,求实数
为假,求实数![]() 的取值范围.
的取值范围.
【答案】![]() 或
或![]()
【解析】
根据“![]() 或
或![]() 为真,
为真,![]() 为假”判断出“
为假”判断出“![]() 为真,
为真,![]() 为假”,利用判别式列不等式分别求得
为假”,利用判别式列不等式分别求得![]() 为假、
为假、![]() 为真时
为真时![]() 的取值范围,再取两者的交集求得实数
的取值范围,再取两者的交集求得实数![]() 的取值范围.
的取值范围.
因为![]() 或
或![]() 为真,
为真,![]() 为假,所以
为假,所以![]() 为真,
为真,![]() 为假
为假
![]() 为假,
为假,![]() ,即:
,即:![]() ,∴
,∴![]() 或
或![]() ,
,
![]() 为真,
为真,![]() ,即:
,即:![]() ,∴
,∴![]() 或
或![]() ,
,
所以取交集为![]() 或
或![]() .
.
【点睛】
本小题主要考查含有简单逻辑联结词命题的真假性,考查一元二次方程根与判别式的关系,考查一元二次不等式解集为![]() 与判别式的关系,属于中档题.
与判别式的关系,属于中档题.
【题型】解答题
【结束】
18
【题目】已知双曲线的中心在原点,焦点为![]() ,
,![]() 且离心率
且离心率![]() .
.
(1)求双曲线的方程;
(2)求以点![]() 为中点的弦所在的直线方程.
为中点的弦所在的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() .
.
(1)求函数f(x)的单调增区间.
(2)若方程![]() 上有解,求实数m的取值范围.
上有解,求实数m的取值范围.
(3)设![]() ,已知区间[a,b](a,b∈R且a<b)满足:y=g(x)在[a,b]上至少含有100个零点,在所有满足上述条件的[a,b]中求b﹣a的最小值.
,已知区间[a,b](a,b∈R且a<b)满足:y=g(x)在[a,b]上至少含有100个零点,在所有满足上述条件的[a,b]中求b﹣a的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com