
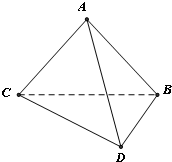
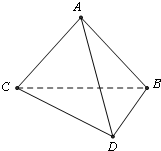
 如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.
如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.| 3 |
| 2 |
| AB2+DB2 |
| 30 |
 ,
,| 3 |
| 2 |
| 2 |
| 3 |
| AB2+DB2 |
| 30 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
6
| ||
| 5 |
6
| ||
| 5 |


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
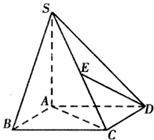 已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,SA=AB=AD=2,
已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,SA=AB=AD=2,查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,底面为矩形ABCD,E,F分别为AB,PC的中点,且PD=PE,PB=PC,求证:
如图,在四棱锥P-ABCD中,底面为矩形ABCD,E,F分别为AB,PC的中点,且PD=PE,PB=PC,求证:查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
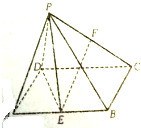
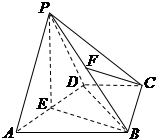 如图,在四棱锥P-ABCD中,侧面PAD是等边三角形,AB∥CD,AB=2CD,BC⊥CD,∠DBC=30°,点E,F分别为AD,PB的中点.
如图,在四棱锥P-ABCD中,侧面PAD是等边三角形,AB∥CD,AB=2CD,BC⊥CD,∠DBC=30°,点E,F分别为AD,PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| A、函数f(x)的最小正周期为π | ||
B、函数f(x)在区间[0,
| ||
| C、函数f(x)的图象关于直线x=0对称 | ||
D、函数f(x+
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com