
【题目】已知点![]() ,
,![]() 是圆
是圆![]() 上的一个动点,
上的一个动点,![]() 为圆心,线段
为圆心,线段![]() 的垂直平分线与直线
的垂直平分线与直线![]() 的交点为
的交点为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() 两点(
两点(![]() 不经过
不经过![]() 点),且
点),且![]() ,证明:直线
,证明:直线![]() 经过定点,并写出该定点的坐标.
经过定点,并写出该定点的坐标.
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,![]() (万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某学校研究性课题《什么样的活动最能促进同学们进行垃圾分类》向题的统计图(每个受访者都只能在问卷的5个活动中选择一个),以下结论错误的是( )

A. 回答该问卷的总人数不可能是100个
B. 回答该问卷的受访者中,选择“设置分类明确的垃圾桶”的人数最多
C. 回答该问卷的受访者中,选择“学校团委会宣传”的人数最少
D. 回答该问卷的受访者中,选择“公益广告”的人数比选择“学校要求”的少8个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长均相等的正四棱锥![]() 中,
中, ![]() 为底面正方形的重心,
为底面正方形的重心, ![]() 分别为侧棱
分别为侧棱![]() 的中点,有下列结论:
的中点,有下列结论:
①![]() 平面
平面![]() ;②平面
;②平面![]() 平面
平面![]() ;③
;③![]() ;
;
④直线![]() 与直线
与直线![]() 所成角的大小为
所成角的大小为![]() .
.
其中正确结论的序号是__________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)·g(x)+f(x)·g′(x)>0,且f(-3)·g(-3)=0,则不等式f(x)·g(x)<0的解集是( )
A. (-3,0)∪(3,+∞)
B. (-3,0)∪ (0,3)
C. (-∞,-3)∪(3,+∞)
D. (-∞,-3)∪(0,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 折起,使
折起,使![]() ,连接
,连接![]() ,得到如图所示的几何体.
,得到如图所示的几何体.
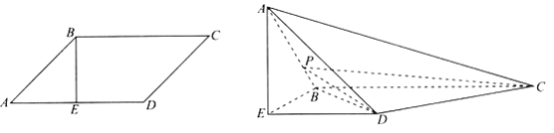
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若点![]() 在线段
在线段![]() 上,直线
上,直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A,B,C所对的边分别为a,b,c且ccosA=4,asinC=5.
(1)求边长c;
(2)著△ABC的面积S=20.求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com