Question

7．已知函数f（x）=$\frac{{e}^{x}}{|x|}$，关于x的方程f²（x）+（m+1）f（x）+m+4=0（m∈R）有四个相异的实数根，则m的取值范围是（　　）

• A． （-4，-e-$\frac{4}{e+1}$）
• B． （-4，-3）
• C． （-e-$\frac{4}{e+1}$，-3）
• D． （-e-$\frac{4}{e+1}$，+∞）

Answer 1

分析 求函数的导数，判断函数的取值情况，利用换元法，设t=f（x），将方程转化为一元二次方程，利用根的分布建立条件关系即可得到结论．

解答 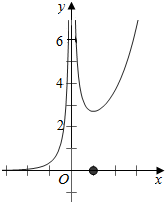解：f（x）=$\frac{{e}^{x}}{|x|}$=$\left\{\begin{array}{l}{\frac{{e}^{x}}{x}，x＞0}\\{-\frac{{e}^{x}}{x}，x＜0}\end{array}\right.$，
由x＞0时，f（x）=$\frac{{e}^{x}}{x}$的导数为f′（x）=$\frac{{e}^{x}（x-1）}{{x}^{2}}$，
可得x＞1，f（x）递增，0＜x＜1时f（x）递减，x=1处取得极小值e；
当x＜0时，f（x）=-$\frac{{e}^{x}}{x}$的导数为f′（x）=-$\frac{{e}^{x}（x-1）}{{x}^{2}}$，
可得x＜0时f（x）递增，
作出函数f（x）对应的图象如图：
设t=f（x），方程f²（x）+（m+1）f（x）+m+4=0
等价为t²+（m+1）t+m+4=0，
由题意结合图象可得△＞0，且0＜t₁＜e且t₂＞e，
即有（m+1）²-4（m+4）＞0，解得m＞5或m＜-3，①
由f（t）=t²+（m+1）t+m+4，可得f（0）＞0，f（e）＜0，
即为m＞-4，m＜-e-$\frac{4}{e+1}$，②
由①②可得-4＜m＜-e-$\frac{4}{e+1}$．
故选：A．

点评 本题考查了根的存在性及根的个数的判断，考查了利用函数的导函数分析函数的单调性，考查了学生分析问题和解决问题的能力，利用换元法转化为一元二次方程，是解决本题的关键．