
分析 (1)化简f(x)的解析式,得出f(x)的单调性,利用单调性求出f(x)的最小值;
(2)计算[g(a)+g(b)]2,利用基本不等式即可得出结论.
解答 解:(1)f(x)=|x-1|+|x-5|=$\left\{\begin{array}{l}{-2x+6,x≤1}\\{4,1<x<5}\\{2x-6,x≥5}\end{array}\right.$,
∴f(x)在(-∞,1]上单调递减,在[5,+∞)上单调递增,
∵f(1)=4,f(5)=4,
∴f(x)的最小值为4.
(2)证明:由(1)可知m=4,
g(a)+g(b)=$\sqrt{1+{a}^{2}}$+$\sqrt{1+{b}^{2}}$,
∴[g(a)+g(b)]2=1+a2+1+b2+2$\sqrt{(1+{a}^{2})(1+{b}^{2})}$=8+2$\sqrt{(1+{a}^{2})(1+{b}^{2})}$,
∵$\sqrt{(1+{a}^{2})(1+{b}^{2})}$≤$\frac{1+{a}^{2}+1+{b}^{2}}{2}$=4,
∴[g(a)+g(b)]2≤16,
∴g(a)+g(b)≤4.
点评 本题考查了函数的单调性,分段函数的最值计算,基本不等式的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
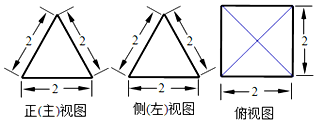
| A. | 16 | B. | 12 | C. | $\frac{4\sqrt{3}}{3}$+4 | D. | 4$\sqrt{3}$+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
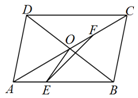 已知平行四边形ABCD中,$|\overrightarrow{AB}|=3$,$|\overrightarrow{AD}|=2$,对角线AC交BD于点O,AB上一点E满足$\overrightarrow{OE}•\overrightarrow{BD}=0$,F为AC上任意一点.
已知平行四边形ABCD中,$|\overrightarrow{AB}|=3$,$|\overrightarrow{AD}|=2$,对角线AC交BD于点O,AB上一点E满足$\overrightarrow{OE}•\overrightarrow{BD}=0$,F为AC上任意一点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 我国古代,9是数字之极,代表尊贵之意,所以中国古代皇家建筑中包含许多与9相关的设计.例如,北京天坛圆丘的地面由扇环形的石板铺成(如图所示),最高一层是一块天心石,围绕它的第一圈有9块石板,从第二圈开始,每一圈比前一圈多9块,共有9圈,则前9圈的石板总数是405.
我国古代,9是数字之极,代表尊贵之意,所以中国古代皇家建筑中包含许多与9相关的设计.例如,北京天坛圆丘的地面由扇环形的石板铺成(如图所示),最高一层是一块天心石,围绕它的第一圈有9块石板,从第二圈开始,每一圈比前一圈多9块,共有9圈,则前9圈的石板总数是405.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | $\frac{9}{2}$ | C. | $-\frac{5}{2}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3\overrightarrow i+2\overrightarrow j$ | B. | $-2\overrightarrow i+3\overrightarrow j$ | C. | $-3\overrightarrow i+2\overrightarrow j$ | D. | $2\overrightarrow i-3\overrightarrow j$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com