
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)设函数![]() ,若函数
,若函数![]() 恰有一个零点,求函数
恰有一个零点,求函数![]() 的解析式.
的解析式.
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】某工厂加工产品![]() 的工人的年龄构成和相应的平均正品率如下表:
的工人的年龄构成和相应的平均正品率如下表:
年龄(单位:岁) |
|
|
|
|
人数比例 | 0.3 | 0.4 | 0.2 | 0.1 |
平均正品率 | 85% | 95% | 80% | 70% |
(1)画出该工厂加工产品![]() 的工人的年龄频率分布直方图;
的工人的年龄频率分布直方图;
(2)估计该工厂工人加工产品![]() 的平均正品率;
的平均正品率;
(3)该工厂想确定一个转岗年龄![]() 岁,到达这个年龄的工人不再加工产品
岁,到达这个年龄的工人不再加工产品![]() ,转到其他岗位,为了使剩余工人加工产品
,转到其他岗位,为了使剩余工人加工产品![]() 的平均正品率不低于90%,若年龄在同一区间内的工人加工产品
的平均正品率不低于90%,若年龄在同一区间内的工人加工产品![]() 的正品率都取相应区间的平均正品率,则估计
的正品率都取相应区间的平均正品率,则估计![]() 最高可定为多少岁?
最高可定为多少岁?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】出版商为了解某科普书一个季度的销售量![]() (单位:千本)和利润
(单位:千本)和利润![]() (单位:元/本)之间的关系,对近年来几次调价之后的季销售量进行统计分析,得到如下的10组数据.
(单位:元/本)之间的关系,对近年来几次调价之后的季销售量进行统计分析,得到如下的10组数据.
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2.4 | 3.1 | 4.6 | 5.3 | 6.4 | 7.1 | 7.8 | 8.8 | 9.5 | 10 |
| 18.1 | 14.1 | 9.1 | 7.1 | 4.8 | 3.8 | 3.2 | 2.3 | 2.1 | 1.4 |
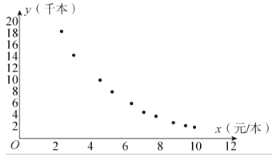
根据上述数据画出如图所示的散点图:
(1)根据图中所示的散点图判断![]() 和
和![]() 哪个更适宜作为销售量
哪个更适宜作为销售量![]() 关于利润
关于利润![]() 的回归方程类型?(给出判断即可,不需要说明理由)
的回归方程类型?(给出判断即可,不需要说明理由)
(2)根据(1)中的判断结果及参考数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)根据回归方程预测当每本书的利润为10.5元时的季销售量.
参考公式及参考数据:
①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的公式分别为
的斜率和截距的公式分别为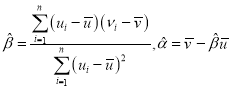 .
.
②参考数据:
|
|
|
|
|
|
|
6.50 | 6.60 | 1.75 | 82.50 | 2.70 |
|
|
表中![]() .另:
.另:![]() .计算时,所有的小数都精确到0.01.
.计算时,所有的小数都精确到0.01.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,动点
中,动点![]() 与两定点
与两定点![]() ,
,![]() 连线的斜率之积为
连线的斜率之积为![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知点![]() ,过原点
,过原点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点(点
两点(点![]() 在第一象限),求四边形
在第一象限),求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 月份的二中迎来了国内外的众多宾客,其中很多人喜欢询问
月份的二中迎来了国内外的众多宾客,其中很多人喜欢询问![]() 团队模式,为了了解“询问
团队模式,为了了解“询问![]() 团队模式”是否与性别有关,在
团队模式”是否与性别有关,在![]() 月期间,随机抽取了
月期间,随机抽取了![]() 人,得到如下所示的列联表:
人,得到如下所示的列联表:
关心“ | 不关心“ | 合计 | |
男性 | 12 | ||
女性 | 36 | ||
合计 | 80 |
(1)若在![]() 这人中,按性别分层抽取一个容量为
这人中,按性别分层抽取一个容量为![]() 的样本,男性应抽
的样本,男性应抽![]() 人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过
人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过![]() 前提下,认为关心“
前提下,认为关心“![]() 团队”与性别有关系?
团队”与性别有关系?
(2)若以抽取样本的频率为概率,从![]() 月来宾中随机抽取
月来宾中随机抽取![]() 人赠送精美纪念品,记这
人赠送精美纪念品,记这![]() 人中关心“
人中关心“![]() 团队”人数为
团队”人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
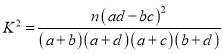
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凤鸣山中学的高中女生体重![]() (单位:kg)与身高
(单位:kg)与身高![]() (单位:cm)具有线性相关关系,根据一组样本数据
(单位:cm)具有线性相关关系,根据一组样本数据![]() (
(![]() ),用最小二乘法近似得到回归直线方程为
),用最小二乘法近似得到回归直线方程为![]() ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.![]() 与
与![]() 具有正线性相关关系
具有正线性相关关系
B.回归直线过样本的中心点![]()
C.若该中学某高中女生身高增加1cm,则其体重约增加0.85kg
D.若该中学某高中女生身高为160cm,则可断定其体重必为50.29kg.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系![]() 的原点为极坐标系的极点,
的原点为极坐标系的极点,![]() 轴的正半轴为极轴.已知曲线
轴的正半轴为极轴.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 是
是![]() 上一动点,
上一动点,![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() 的极坐标方程,并化为直角坐标方程;
的极坐标方程,并化为直角坐标方程;
(2)若点![]() ,直线
,直线![]() 的参数方程
的参数方程![]() (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,当
,当![]() 取最小值时,求直线
取最小值时,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下三个命题:①在匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;②若两个变量的线性相关性越强,则相关系数的绝对值越接近于1;③对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,判断“
越小,判断“![]() 与
与![]() 有关系”的把握越大;其中真命题的个数为( )
有关系”的把握越大;其中真命题的个数为( )
A.3B.2C.1D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com