
【题目】设关于某产品的明星代言费x(百万元)和其销售额y(百万元),有如表的统计表格:
i | 1 | 2 | 3 | 4 | 5 | 合计 |
xi(百万元) | 1.26 | 1.44 | 1.59 | 1.71 | 1.82 | 7.82 |
wi(百万元) | 2.00 | 2.99 | 4.02 | 5.00 | 6.03 | 20.04 |
yi(百万元) | 3.20 | 4.80 | 6.50 | 7.50 | 8.00 | 30.00 |
| ||||||
其中 ![]() .
.
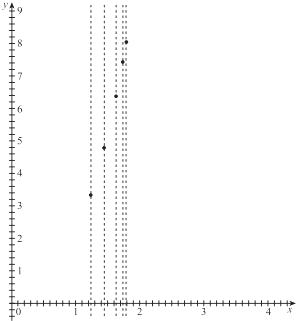
(1)在坐标系中,作出销售额y关于广告费x的回归方程的散点图,根据散点图指出:y=a+blnx,y=c+dx3哪一个适合作销售额y关于明星代言费x的回归类方程(不需要说明理由); 
(2)已知这种产品的纯收益z(百万元)与x,y有如下关系:x=0.2y﹣0.726x(x∈[1.00,2.00]),试写出z=f(x)的函数关系式,试估计当x取何值时,纯收益z取最大值?(以上计算过程中的数据统一保留到小数点第2位)
【答案】
(1)解:散点图如右图:
根据散点图可知,y=c+dx3适合作销售额y关于明星代言费x的回归方程
(2)解:令ω=x3,则y=c+dω是y关于ω的线性回归方程,
所以 ![]() =
= 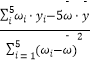 =1.21,
=1.21, ![]() =
= ![]() ﹣1.21ω=1.15+1.21x3,
﹣1.21ω=1.15+1.21x3,
所以y=1.15+1.21ω=1.15+1.21x3.
z=f(x)=0.2y﹣0.726x=0.2(1.15+1.21x3)﹣0.726x
=0.242x3﹣0.726x+0.23,其中x∈[1.00,2.00]
令z'=0.726x2﹣0.726≥0,得x≥1.00,
因为x∈[1.00,2.00],
所以估计当明星代言费x=2.00百万元时,纯收益z取最大值.
估计:当明星代言费x=2.00百万元时,纯收益z取最大值
【解析】(1)散点图,根据散点图可知,y=c+dx3适合作销售额y关于明星代言费x的回归方程.(2)令ω=x3 , 则y=c+dω是y关于ω的线性回归方程,求出y=1.15+1.21ω=1.15+1.21x3 . z=f(x)=0.242x3﹣0.726x+0.23,其中x∈[1.00,2.00],利用导数性质求出当明星代言费x=2.00百万元时,纯收益z取最大值.
【考点精析】关于本题考查的频率分布直方图,需要了解频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】某中学对男女学生是否喜爱古典音乐进行了一个调查,调查者对学校高三年级随机抽取了100名学生,调查结果如表:
喜爱 | 不喜爱 | 总计 | |
男学生 | 60 | 80 | |
女学生 | |||
总计 | 70 | 30 |
附:K2= ![]()
P(K2≥k0) | 0.100 | 0.050 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |
(1)完成如表,并根据表中数据,判断是否有95%的把握认为“男学生和女学生喜欢古典音乐的程度有差异”;
(2)从以上被调查的学生中以性别为依据采用分层抽样的方式抽取10名学生,再从这10名学生中随机抽取5名学生去某古典音乐会的现场观看演出,求正好有X个男生去观看演出的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示是某条公共汽车路线收支差额y与乘客量x的图象(收支差额=车票收入—支出费用)由于目前本条线路在亏损,公司有关人员提出了两条建议:
建议(Ⅰ)是不改变车票价格,减少支出费用;建议(Ⅱ)是不改变支出费用,提高车票价格. 图中虚线表示调整前的状态,实线表示调整后的状态. 在上面四个图象中
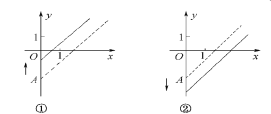

A. ①反映了建议(Ⅱ),③反映了建议(Ⅰ) B. ①反映了建议(Ⅰ),③反映了建议(Ⅱ)
C. ②反映了建议(Ⅰ),④反映了建议(Ⅱ) D. ④反映了建议(Ⅰ),②反映了建议(Ⅱ)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信支付诞生于微信红包,早期知识作为社交的一部分“发红包”而诞生的,在发红包之余才发现,原来微信支付不仅可以用来发红包,还可以用来支付,现在微信支付被越来越多的人们所接受,现从某市市民中随机抽取300为对是否使用微信支付进行调查,得到下列![]() 的列联表:
的列联表:
年轻人 | 非年轻人 | 总计 | |
经常使用微信支付 | 165 | 225 | |
不常使用微信支付 | |||
合计 | 90 | 300 |
根据表中数据,我们得到的统计学的结论是:由__________的把握认为“使用微信支付与年龄有关”。
|
|
|
|
|
|
|
|
|
|
|
|
其中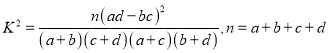
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了创建全国文明城市,面向社会招募志愿者,现从20岁至50岁的志愿者中按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示,若用分层抽样的方法从这些志愿者中抽取20人参加“创建全国文明城市验收日”的活动。
,得到的频率分布直方图如图所示,若用分层抽样的方法从这些志愿者中抽取20人参加“创建全国文明城市验收日”的活动。
(1)求从第2组和第3组中抽取的人数分别是多少;
(2)若小李和小王都是32岁,同时参加了“创建全国文明城市验收日”的活动,现要从第3组抽取的人中临时抽调两人去执行另一任务,求小李和小王至少有一人被抽调的概率。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() 表示
表示![]() ,
,![]() 中的最大值,如
中的最大值,如![]()
![]() .已知函数
.已知函数![]() ,
,![]() .
.
(1)设![]() ,求函数
,求函数![]() 在
在![]() 上零点的个数;
上零点的个数;
(2)试探讨是否存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com