
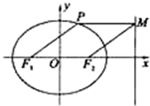
 如图,点P在椭圆
如图,点P在椭圆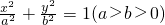 上,F1、F2分别是椭圆的左、右焦点,过点P作椭圆右准线的垂线,垂足为M,若四边形PF1F2M为菱形,则椭圆的离心率是
上,F1、F2分别是椭圆的左、右焦点,过点P作椭圆右准线的垂线,垂足为M,若四边形PF1F2M为菱形,则椭圆的离心率是

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源:2010-2011学年广西省高三高考模拟考试文数 题型:填空题
如图,点P在椭圆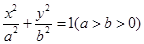 上,F1、F2分别
上,F1、F2分别
是椭圆的左、右焦点,过点P作椭圆右准线的垂线,垂足为M,
若四边形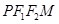 为菱形,则椭圆的离心率是
为菱形,则椭圆的离心率是

查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省武汉市黄陂一中盘龙校区高二数学检测试卷(六)(解析版) 题型:填空题
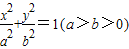 上,F1、F2分别是椭圆的左、右焦点,过点P作椭圆右准线的垂线,垂足为M,若四边形PF1F2M为菱形,则椭圆的离心率是 .
上,F1、F2分别是椭圆的左、右焦点,过点P作椭圆右准线的垂线,垂足为M,若四边形PF1F2M为菱形,则椭圆的离心率是 .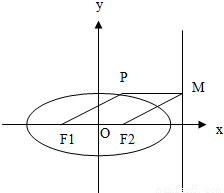
查看答案和解析>>
科目:高中数学 来源:2011年广西省桂林中学高考数学模拟试卷(文科)(解析版) 题型:填空题
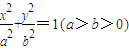 上,F1、F2分别是椭圆的左、右焦点,过点P作椭圆右准线的垂线,垂足为M,若四边形PF1F2M为菱形,则椭圆的离心率是 .
上,F1、F2分别是椭圆的左、右焦点,过点P作椭圆右准线的垂线,垂足为M,若四边形PF1F2M为菱形,则椭圆的离心率是 .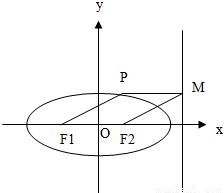
查看答案和解析>>
科目:高中数学 来源:2011年四川省高三摸底数学试卷1(文科)(解析版) 题型:选择题
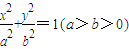 上,F1、F2分别是椭圆的左、右焦点,过点P作椭圆右准线的垂线,垂足为M,若四边形PF1F2M为菱形,则椭圆的离心率是( )
上,F1、F2分别是椭圆的左、右焦点,过点P作椭圆右准线的垂线,垂足为M,若四边形PF1F2M为菱形,则椭圆的离心率是( )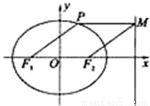
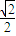
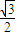

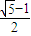
查看答案和解析>>
科目:高中数学 来源:期末题 题型:填空题
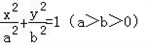 上,F1、F2分别是椭圆的左、右焦点,过点P作椭圆右准线的垂线,垂足为M,若四边形PF1F2M为菱形,则椭圆的离心率是( )
上,F1、F2分别是椭圆的左、右焦点,过点P作椭圆右准线的垂线,垂足为M,若四边形PF1F2M为菱形,则椭圆的离心率是( )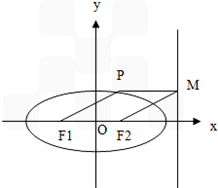
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com