
����Ŀ�����壺������{an}�г�ȡm��m��N��m��3�������{an}�еĴ��������γ�һ��������{bn}�����{bn}Ϊ{an}�������У���{bn}�ɵȲ��ȱȣ������{bn}Ϊ{an}�ĵȲ��ȱȣ������У�
��1��������{an}��ǰn���ΪSn����֪![]() ��
��
��������{an}��ͨ�ʽ��
������{an}�Ƿ���ڵȲ������У������ڣ�����Ȳ������У��������ڣ���˵�����ɣ�
��2����֪����{an}��ͨ�ʽΪan��n+a��a��Q+����֤����{an}���ڵȱ������У�
���𰸡���1����![]() ���ڲ����ڵȲ������У���������2��������
���ڲ����ڵȲ������У���������2��������
��������
��1���ٸ���![]() ����n��1ʱ��
����n��1ʱ��![]() ����n��2ʱ���õ�
����n��2ʱ���õ�![]() ����ʽ�������.�ڼ��������{an}�г�3��ak��al��am��k��l��m���ɵȲ���õȲ�������2al��ak+am����2��2l��1��2k��1+2m��1��
����ʽ�������.�ڼ��������{an}�г�3��ak��al��am��k��l��m���ɵȲ���õȲ�������2al��ak+am����2��2l��1��2k��1+2m��1��
����ã�2��2l��k��1+2m��k����������ż���ж�.���������{an}�г�m��m��N��m��4�����ǰ����سɵȲ����У���������֤.
��2����������{an}�д���3��n0+a��n0+a+k��n0+a+l��k��l���ɵȱȣ���n0+a��b����b��Q+���ʿ���![]() ��p��q�ǻ��ʵ��������������ݵȱ������
��p��q�ǻ��ʵ��������������ݵȱ������![]() ����
����![]() ��ȡk��q����l��2k+pq������֤��b+k��2=b��b+l���Ƿ��������.
��ȡk��q����l��2k+pq������֤��b+k��2=b��b+l���Ƿ��������.
��1������Ϊ![]() �����Ե�n��1ʱ��
�����Ե�n��1ʱ��![]() ��
��
��n��2ʱ��![]() ������
������![]() ��
��
���Ͽ�֪��![]() ��
��
�ڼ��������{an}�г�3��ak��al��am��k��l��m���ɵȲ
��2al��ak+am����2��2l��1��2k��1+2m��1��
����ã�2��2l��k��1+2m��k��
��Ϊk��l��m������l��k��0��m��k��0����l��k��m��k����������
����2��2l��kΪż����1+2m��kΪ����������2��2l��k��1+2m��k��������
��ˣ�����{an}����������Ȳ������У�
��������{an}�г�m��m��N��m��4�����ǰ����سɵȲ����У���������
���Ͽ�֪������{an}�����ڵȲ������У�
��2����������{an}�д���3��n0+a��n0+a+k��n0+a+l��k��l���ɵȱȣ�
��n0+a��b����b��Q+���ʿ���![]() ��p��q�ǻ��ʵ�����������
��p��q�ǻ��ʵ�����������
��������![]() ��
��
�������㣨b+k��2��b��b+l������������![]() ��
��
ȡk��q����l��2k+pq��
��ʱ![]() ��
��![]() ��
��
�ʴ�ʱ��b+k��2��b��b+l��������
�������{an}�д���3��n0+a��n0+a+k��n0+a+l��k��l���ɵȱȣ�
��������{an}���ڵȱ������У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �����ֵΪ
�����ֵΪ![]() ��������
��������![]() ��x��0����������ֱ��
��x��0����������ֱ��![]() ƽ�У�����eΪ��Ȼ�����ĵ�������
ƽ�У�����eΪ��Ȼ�����ĵ�������
��1����ʵ��a��b��ֵ��
��2�����![]() ����
����![]() ����֤��
����֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ļ����˻��Ƴ���2021��7��23����8��8�վ��У��˴ΰ��˻Ὣ����4![]() 100����Ů��Ӿ��������һ�µı�����Ŀ�������Ĺ����ǣ�ÿ�����������ɳ�2��2Ů����4���˶�Ա�μӱ�����������Ӿ
100����Ů��Ӿ��������һ�µı�����Ŀ�������Ĺ����ǣ�ÿ�����������ɳ�2��2Ů����4���˶�Ա�μӱ�����������Ӿ![]() ��Ӿ
��Ӿ![]() ��Ӿ
��Ӿ![]() ����Ӿ�Ľ���˳��ÿ��Ӿ��100������1���˶�Ա��ɣ���ÿ���˶�Ա��Ҫ����.���й���ȷ���˱�ս����Ŀ��4���˶�Ա����������Ů�˶�Ա��ֻ�ܳе���Ӿ��������Ӿ�����˶�Ա��ֻ�ܳе���Ӿ������Ӿ��ʣ��2���˶�Ա����Ӿ�˶����Գе������й��Ӳ����İ��Ź��У� ��
����Ӿ�Ľ���˳��ÿ��Ӿ��100������1���˶�Ա��ɣ���ÿ���˶�Ա��Ҫ����.���й���ȷ���˱�ս����Ŀ��4���˶�Ա����������Ů�˶�Ա��ֻ�ܳе���Ӿ��������Ӿ�����˶�Ա��ֻ�ܳе���Ӿ������Ӿ��ʣ��2���˶�Ա����Ӿ�˶����Գе������й��Ӳ����İ��Ź��У� ��
A.144��B.8��C.24��D.12��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����X��������tΪ��������F�ǰ���t���Ӽ����Ӽ��壺F=![]() .���F�еIJ����Ӽ����ɵļ���S���㣺��S��������������ȵļ���A��B��
.���F�еIJ����Ӽ����ɵļ���S���㣺��S��������������ȵļ���A��B��![]() �������������SΪ����.��S1Ϊ�����������ķ�����S2�����ⷴ��.֤��������S2��S1�ĵ���f������
�������������SΪ����.��S1Ϊ�����������ķ�����S2�����ⷴ��.֤��������S2��S1�ĵ���f������![]() ��
��![]() ����.
����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ����Ϊ
����Ϊ![]() ��
��![]() ������
Ϊ������![]() �Ҵ�ֱ��
�Ҵ�ֱ��![]() ���������
���������![]() ���ң���֪��
���ң���֪��![]() Ϊֱ����Բ������
Ϊֱ����Բ������![]() .
.
��1����![]() ��ֵ����Բ�ķ��̣�
��ֵ����Բ�ķ��̣�
��2����![]() Ϊ
Ϊ![]() ������һ�㣬����
������һ�㣬����![]() ��
��![]() �����ߣ��е�Ϊ
�����ߣ��е�Ϊ![]() ��֤����
��֤����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ׯ��˵����һ��֮������ȡ��룬��������������仰��������һ���������⣬���ó����ͼ��������ͼ��ʾ��������ij��������n�������S�ʣ�![]() ��
��![]() �����������n��ֵΪ��������
�����������n��ֵΪ��������
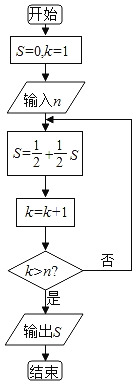
A.7B.6C.5D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����axlnx��x2��ax+1��a��R���ڶ���������������ͬ�ļ�ֵ��.
��1����ʵ��a��ȡֵ��Χ��
��2����������ֵ��ֱ�Ϊx1��x2��x1��x2��֤����f��x1��+f��x2����2��x12+x22.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ԲC:![]() ��ԭ���ֱ������Բ����A��B����(��A�ڵ�һ����)������A��x��Ĵ��ߣ�����Ϊ��
��ԭ���ֱ������Բ����A��B����(��A�ڵ�һ����)������A��x��Ĵ��ߣ�����Ϊ��![]() ����ֱ��BE����Բ����һ����ΪP������AP�õ�ֱ��l����x���ڵ�M����y���ڵ�N.
����ֱ��BE����Բ����һ����ΪP������AP�õ�ֱ��l����x���ڵ�M����y���ڵ�N.
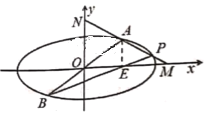
��1����![]() ����ֱ��AP��б�ʣ�
����ֱ��AP��б�ʣ�
��2����![]() ������ֱ�ΪS1��S2��S3����
������ֱ�ΪS1��S2��S3����![]() �ĵ����ֵ.
�ĵ����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() Ϊ
Ϊ![]() �е㣬��
�е㣬��![]() ��
��![]() ��������
��������![]() .
.
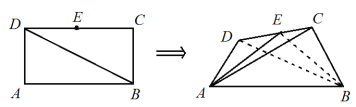
��1����![]() ʱ����֤��
ʱ����֤��![]() ��
��
��2����![]() ʱ��������
ʱ��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com