Question

已知关于x的方程x²-2mx+m+6=0的两个根为x₁，x₂，求函数y=（x₁-1）²+（x₂-1）²的最小值．

Answer 1

解：∵方程x²-2mx+m+6=0的两个根为x₁，x₂，
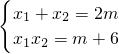
∴且△=4（m²-m-6）≥0，
∴y=（x₁-1）²+（x₂-1）²=（x₁+x₂）²-2x₁x₂-2（x₁+x₂）+2=4m²-6m-10，
且m≥3或m≤-2．
由二次函数的性质知，当m=3时，
函数y=4m²-6m-10的取得最小值，最小值为：8．
即函数y=（x₁-1）²+（x₂-1）²的最小值是8．
分析：先根据根与系数的关系利用参数m表示出函数的解析式，必须注意参数m的取值范围，再结合二次函数的图象与性质求出最小值即可．
点评：本题主要考查了二次方程根与系数的关系、二次函数最值等函数与方程的综合运用．