
【题目】![]()
(1)求![]() 在
在![]() 上的单调区间;
上的单调区间;
(2)当![]() 时,设函数
时,设函数![]() ,
,![]() 时,证明
时,证明![]() .
.
(3)证明:![]() .
.
【答案】(1)见解析(2)见解析(3)见解析
【解析】
(1)分别在![]() 、
、![]() 、
、![]() 和
和![]() 四种情况下,根据导函数的正负确定原函数的单调区间;
四种情况下,根据导函数的正负确定原函数的单调区间;
(2)将所证不等式转化为证明![]() ,采用换元法可知即证
,采用换元法可知即证![]() ,利用导数可确定函数单调性,进而确定
,利用导数可确定函数单调性,进而确定![]() ,由此证得结论;
,由此证得结论;
(3)由![]() 可得
可得![]() ,通过分离常数法进行配凑,可以得到
,通过分离常数法进行配凑,可以得到![]() ,根据不等式的性质,结合累加的方法可证得结论.
,根据不等式的性质,结合累加的方法可证得结论.
(1)由题意得: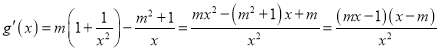 ,
,
①当![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,
![]() 的单调递减区间为
的单调递减区间为![]() ,无单调递增区间;
,无单调递增区间;
②当![]() 时,令
时,令![]() ,解得:
,解得:![]() 或
或![]() (舍),
(舍),
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
③当![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,
![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间;
,无单调递减区间;
④当![]() 时,令
时,令![]() ,解得:
,解得:![]() (舍)或
(舍)或![]()
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
综上所述:当![]() 时,
时,![]() 的单调递减区间为
的单调递减区间为![]() ,无单调递增区间;
,无单调递增区间;
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间;
,无单调递减区间;
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)由题意得:![]() ,
,
![]() ,
,![]() ,即
,即![]() ,
,
要证![]() ,需证
,需证![]() ,即证
,即证![]() ,
,
设![]() ,则要证
,则要证![]() ,等价于证:
,等价于证:![]() ,
,
令![]() ,则
,则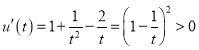 ,
,
![]() 在区间
在区间![]() 内单调递增,
内单调递增,![]() ,
,
即![]() ,故
,故![]() .
.
(3)由(1)知:当![]() 时,
时,![]() 在
在![]() 上为增函数,
上为增函数,![]() ,
,
即![]() ,
,
令![]() , 可得:
, 可得:![]() ,
,
即![]() ,
,
![]()
![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
不等式左右分别相加得:
![]()
![]()
![]() ,不等式得证.
,不等式得证.


科目:高中数学 来源: 题型:
【题目】十九大提出,加快水污染防治,建设美丽中国.根据环保部门对某河流的每年污水排放量![]() (单位:吨)的历史统计数据,得到如下频率分布表:
(单位:吨)的历史统计数据,得到如下频率分布表:

将污水排放量落入各组的频率作为概率,并假设每年该河流的污水排放量相互独立.
(1)求在未来3年里,至多1年污水排放量![]() 的概率;(2)该河流的污水排放对沿河的经济影响如下:当
的概率;(2)该河流的污水排放对沿河的经济影响如下:当![]() 时,没有影响;当
时,没有影响;当![]() 时,经济损失为10万元;当
时,经济损失为10万元;当![]() 时,经济损失为60万元.为减少损失,现有三种应对方案:
时,经济损失为60万元.为减少损失,现有三种应对方案:
方案一:防治350吨的污水排放,每年需要防治费3.8万元;
方案二:防治310吨的污水排放,每年需要防治费2万元;
方案三:不采取措施.
试比较上述三种文案,哪种方案好,并请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着共享单车的成功运营,更多的共享产品逐步走人大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷,某公司随机抽取1000人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的1000人中的性别以及意见进行了分类,得到的数据如下表所示:
男 | 女 | 总计 | |
认为共享产品对生活有益 |
|
|
|
认为共享产品对生活无益 |
|
|
|
总计 |
|
|
|
(1)求出表格中![]() 的值,并根据表中的数据,判断能否在犯错误的概率不超过
的值,并根据表中的数据,判断能否在犯错误的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(2)现按照分层抽样从认为共享产品对生活无益的人员中随机抽取6人,再从6人中随机抽取2人赠送超市购物券作为答谢,求恰有1人是女性的概率.
参考公式: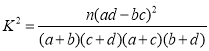 .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程:
已知极坐标系的极点在直角坐标系的原点,极轴与x轴非负半轴重合,直线l的参数方程为:![]() (t为参数,a∈[0,π),曲线C的极坐标方程为:p=2cosθ.
(t为参数,a∈[0,π),曲线C的极坐标方程为:p=2cosθ.
(Ⅰ)写出曲线C在直角坐标系下的标准方程;
(Ⅱ)设直线l与曲线C相交PQ两点,若|PQ|![]() ,求直线l的斜率.
,求直线l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司准备在2020年年初将两千万投资东营经济开发区的“示范区”新型物流,商旅文化两个项目中的一个之中.
项目一:新型物流仓是为企业提供仓储、运输、配送、货运信息等综合物流服务的平台.现准备投资建设10个新型物流仓,每个物流仓投资0.2千万元,假设每个物流仓盈利是相互独立的,据市场调研,到2022年底每个物流仓盈利的概率为![]() ,若盈利则盈利为投资额的40%,否则盈利额为0.
,若盈利则盈利为投资额的40%,否则盈利额为0.
项目二:购物娱乐广场是一处融商业和娱乐于一体的现代化综合服务广场.据市场调研,投资到该项目上,到2022年底可能盈利投资额的50%,也可能亏损投资额的30%,且这两种情况发生的概率分别为![]() 和
和![]() .
.
(1)若投资项目一,记![]() 为盈利的物流仓的个数,求
为盈利的物流仓的个数,求![]() (用
(用![]() 表示);
表示);
(2)若投资项目二,记投资项目二的盈利为![]() 千万元,求
千万元,求![]() (用
(用![]() 表示);
表示);
(3)在(1)(2)两个条件下,针对以上两个投资项目,请你为投资公司选择一个项目,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (t为参数),直线
(t为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).设
为参数).设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,
变化时,![]() 的轨迹为曲线
的轨迹为曲线![]()
(1)写出![]() 的普通方程;
的普通方程;
(2)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,设
轴正半轴为极轴建立极坐标系,设![]() ,
,![]() 为
为![]() 与
与![]() 的交点,求
的交点,求![]() 的极径.
的极径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C:![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]() .
.
(1)求点P的轨迹方程;
(2)设点Q在直线![]() 上,且
上,且![]() 。证明:过点P且垂直于OQ的直线l过C的左焦点F.
。证明:过点P且垂直于OQ的直线l过C的左焦点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 与曲线
与曲线![]() 公共点的极坐标;
公共点的极坐标;
(2)设过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com