
(本题满分14分)某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2000平方米的楼房。经测算,如果将楼房建为x(x ≥ 10)层,则每平方米的平均建筑费用为560 + 48x(单位:元).⑴写出楼房平均综合费用y关于建造层数x的函数关系式;
⑵该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少?
(注:平均综合费用 = 平均建筑费用 + 平均购地费用,平均购地费用 = )
(Ⅰ) y = 560 + 48x + (x ≥ 10,x ∈N*) (Ⅱ) 最少值为2000元
⑴设楼房每平方米的平均综合费为y元,依题意得y = (560 + 48x) + = 560 + 48x + (x ≥ 10,x ∈N*); 5分定义域不对扣1-2分
⑵法一:∵x > 0,∴ 48x + ≥ 2 = 1440, 8分
当且仅当48x = ,即 x = 15时取到“=”, 10分
此时,平均综合费用的最小值为560 + 1440 = 2000元. 13分
答:当该楼房建造15层,可使楼房每平方米的平均综合费用最少,最少值为2000元. 14分
法二:先考虑函数 y = 560 + 48x + (x ≥ 10,x ∈R); 7分(定义域不写和不对扣2分)
则y ' = 48 ?? ,令y ' = 0,即48 ?? = 0,解得 x = 15, 10分
当 0 < x < 15时,y ' < 0;当x > 15时,y ' > 0,又15∈N*,
因此,当x = 15时,y取得最小值,ymin = 2000元. 13分
答:当该楼房建造15层,可使楼房每平方米的平均综合费用最少,最少值为2000元. 14分


科目:高中数学 来源:2011-2012学年上海市高三上学期期中考试文科数学试卷 题型:解答题
(本题满分14分)某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本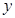 (万元)与年产量
(万元)与年产量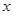 (吨)之间的函数关系式可以近似地表示为
(吨)之间的函数关系式可以近似地表示为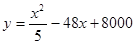 ,已知此生产线年产量最大为210吨.
,已知此生产线年产量最大为210吨.
(1)求年产量为多少吨时,生产每吨产品的平均成本最低,并求最低成本;
(2)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源:广东省09-10学年高二下学期期末考试理科数学试题 题型:解答题
(本题满分14分)某研究小组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试的成绩(百分制)如下表所示:
|
序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
数学成绩 |
95 |
75 |
80 |
94 |
92 |
65 |
67 |
84 |
98 |
71 |
|
物理成绩 |
90 |
63 |
72 |
87 |
91 |
71 |
58 |
82 |
93 |
80 |
|
序号 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
数学成绩 |
67 |
93 |
64 |
78 |
77 |
90 |
57 |
84 |
72 |
83 |
|
物理成绩 |
77 |
82 |
48 |
85 |
69 |
91 |
61 |
82 |
78 |
86 |
若数学成绩90分(含90分)以上为优秀,物理成绩85分(含85分)以上为优秀。
⑴根据上表完成下面的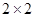 列联表:
列联表:
|
|
数学成绩优秀 |
数学成绩不优秀 |
合计 |
|
物理成绩优秀 |
|
|
|
|
物理成绩不优秀 |
|
12 |
|
|
合计 |
|
|
20 |
⑵根据⑴中表格的数据计算,有多少的把握,认为学生的数学成绩与物理成绩之间有关系?
查看答案和解析>>
科目:高中数学 来源:广东省09-10学年高二下学期期末考试理科数学试题 题型:解答题
(本题满分14分)某学习小组有6个同学,其中4个同学从来没有参加过数学研究性学习活动,2个同学曾经参加过数学研究性学习活动.
(1)现从该小组中任选2个同学参加数学研究性学习活动,求恰好选到1个曾经参加过数学研究性学习活动的同学的概率;
(2)若从该小组中任选2个同学参加数学研究性学习活动,活动结束后,该小组没有参加过数学研究性学习活动的同学个数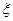 是一个随机变量,求随机变量
是一个随机变量,求随机变量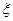 的分布列及数学期望
的分布列及数学期望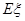 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省温州市高三五校联考数学理卷 题型:解答题
(本题满分14分)某超市为促销商品,特举办“购物有奖100﹪中奖”活动,凡消费者在该超市购物满100元,享受一次摇奖机会,购物满200元,享受两次摇奖机会,以此类推.摇奖机的结构如图所示,将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落。小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,落入A袋为一等奖,奖金为20元,落入B袋为二等奖,奖金为10元,已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是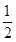
(Ⅰ)求:摇奖两次,均获得一等奖的概率;
(Ⅱ)某消费者购物满200元,摇奖后所得奖金为X元,试求X的分布列与期望;
(Ⅲ)若超市同时举行购物八八折让利于消费者活动(打折后不再享受摇奖),某消费者刚好消费200元,请问他是选择摇奖还是选择打折比较划算.
查看答案和解析>>
科目:高中数学 来源:2010年广东省高三第一次月考文科数学卷 题型:解答题
(本题满分14分)
某校高三的某次数学测试中,对其中100名学生的成绩进行分析,按成绩分组,得到的频率分布表如下:
|
组号 |
分组 |
频数 |
频率 |
|
第1组 |
|
15 |
① |
|
第2组 |
|
② |
0.35 |
|
第3组 |
|
20 |
0.20 |
|
第4组 |
|
20 |
0.20 |
|
第5组 |
|
10 |
0.10 |
|
合计 |
|
100 |
1.00 |
(1)求出频率分布表中①、②位置相应的数据;
(2)为了选拔出最优秀的学生参加即将举行的数学竞赛,学校决定在成绩较高的第3、4、5组中分层抽样取5名学生,则第4、5组每组各抽取多少名学生?
(3)为了了解学生的学习情况,学校又在这5名学生当中随机抽取2名进行访谈,求第4组中至少有一名学生被抽到的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com