
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)证明:当a=3时,函数![]() 有且只有两个零点.
有且只有两个零点.
【答案】(1)分类讨论,详见解析;(2)详见解析.
【解析】
(1)由![]() ,分
,分![]() 和
和![]() 两种情况进行讨论得出函数的单调性.
两种情况进行讨论得出函数的单调性.
(2)函数![]() 有且只有两个零点,即方程
有且只有两个零点,即方程![]() 有且只有两个实数根,即
有且只有两个实数根,即![]() 有且只有两个实数根,设
有且只有两个实数根,设![]() ,求出导数,求出函数
,求出导数,求出函数![]() 的单调区间,结合零点存在原理得出结论,使得问题得证.
的单调区间,结合零点存在原理得出结论,使得问题得证.
解:(1)![]() 的定义域为
的定义域为![]() ,
,![]() .
.
①![]() 时,
时,![]() ,则
,则![]() 在
在![]() 是单调递增;
是单调递增;
②![]() 时,由
时,由![]() 得
得![]() ,当
,当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
综上,![]() 时
时![]() 在
在![]() 是单调递增;
是单调递增;
![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2).![]()
![]()
![]() ,令
,令![]() ,
,
则![]() ,令
,令![]() ,
,
显然![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
![]() ,
,![]()
易知存在唯一![]() ,使
,使![]() ,且
,且![]() 时,
时,![]() ,即
,即![]() ,
,![]() 单调递减;
单调递减;
![]() 时,
时,![]() ,即
,即![]() ,
,![]() 单调递增,
单调递增,
所以![]() 至多有两个零点.又
至多有两个零点.又![]()
![]() ,
,![]() ,
,![]() ,
,
故![]() 在区间
在区间![]() 和
和![]() 各有一个零点.所以函数
各有一个零点.所以函数![]() 有且只有两个零点.
有且只有两个零点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设A,B,C,D为平面内的四点,且A(1,3),B(2,–2),C(4,1).
(1)若![]() ,求D点的坐标;
,求D点的坐标;
(2)设向量![]() ,
,![]() ,若k
,若k![]() –
–![]() 与
与![]() +3
+3![]() 平行,求实数
平行,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足:存在正整数T,对于任意正整数n都有
满足:存在正整数T,对于任意正整数n都有![]() 成立,则称数列
成立,则称数列![]() 为周期数列,周期为T.已知数列
为周期数列,周期为T.已知数列![]() 满足
满足![]() ,
, ,则下列结论中错误的是( )
,则下列结论中错误的是( )
A.若![]() ,则m可以取3个不同的值;
,则m可以取3个不同的值;
B.若![]() ,则数列
,则数列![]() 是周期为3的数列;
是周期为3的数列;
C.对于任意的![]() 且T≥2,存在
且T≥2,存在![]() ,使得
,使得![]() 是周期为
是周期为![]() 的数列
的数列
D.存在![]() 且
且![]() ,使得数列
,使得数列![]() 是周期数列
是周期数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠APC=90°,∠BPD=120°,PB=PD.
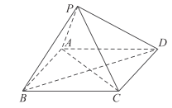
(1)求证:平面APC⊥平面BPD;
(2)若AB=2AP=2,求三棱锥C-PBD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年入冬以来,各地雾霾天气频发,![]() 频频爆表(
频频爆表(![]() 是指直径小于或等于
是指直径小于或等于![]() 微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与
微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与![]() 的浓度是否相关,某市现采集周一到周五某一时间段车流量与
的浓度是否相关,某市现采集周一到周五某一时间段车流量与![]() 的数据如下表:
的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 69 | 70 | 74 | 78 | 79 |
(1)请根据上述数据,在上面给出的坐标系中画出散点图;
(2)试判断![]() 与
与![]() 是否具有线性关系,若有请求出
是否具有线性关系,若有请求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,若没有,请说明理由;
,若没有,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,并在两种坐标系中取相同的长度单位,点
轴的正半轴为极轴,并在两种坐标系中取相同的长度单位,点![]() 的极坐标为
的极坐标为![]() ,圆
,圆![]() 以
以![]() 为圆心,4为半径;又直线
为圆心,4为半径;又直线![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(Ⅰ)求直线![]() 和圆
和圆![]() 的普通方程;
的普通方程;
(Ⅱ)试判定直线![]() 和圆
和圆![]() 的位置关系.若相交,则求直线
的位置关系.若相交,则求直线![]() 被圆
被圆![]() 截得的弦长.
截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年1月10日,引发新冠肺炎疫情的COVID-9病毒基因序列公布后,科学家们便开始了病毒疫苗的研究过程.但是类似这种病毒疫苗的研制需要科学的流程,不是一朝一夕能完成的,其中有一步就是做动物试验.已知一个科研团队用小白鼠做接种试验,检测接种疫苗后是否出现抗体.试验设计是:每天接种一次,3天为一个接种周期.已知小白鼠接种后当天出现抗体的概率为![]() ,假设每次接种后当天是否出现抗体与上次接种无关.
,假设每次接种后当天是否出现抗体与上次接种无关.
(1)求一个接种周期内出现抗体次数![]() 的分布列;
的分布列;
(2)已知每天接种一次花费100元,现有以下两种试验方案:
①若在一个接种周期内连续2次出现抗体即终止本周期试验,进行下一接种周期,试验持续三个接种周期,设此种试验方式的花费为![]() 元;
元;
②若在一个接种周期内出现2次或3次抗体,该周期结束后终止试验,已知试验至多持续三个接种周期,设此种试验方式的花费为![]() 元.
元.
比较随机变量![]() 和
和![]() 的数学期望的大小.
的数学期望的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com