练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （1）计算：C33+C43+C53+…+C103
    （2）证明：Ank+kAnk-1=An+1k．

    解：（1）∵Cmn+Cm-1n=Cmn+1，
    ∴原式=C44+C43+C53+…+C103
    =C54+C53+C63+…+C103
    =C64+C63+C73+…+C103
    =…
    =C104+C103
    =C114
    =330
    （2）证明：∵
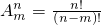
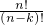
    ∴左边=+k
    =
    =
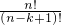
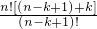
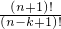
    =An+1k=右边
    分析：（1）先把C33化为C44，再根据组合数的性质，Cnm+Cnm-1=Cn+1m，逐个化简，即可求出C33+C43+C53+…+C103
    的值．
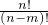
    （2）把左右两边分别用排列数公式，Anm=化简，再判断化简后得式子相等即可．
    点评：本题考查了排列数公式和组合数性质，做题时应认真计算，避免出错．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （1）计算：C33+C43+C53+…+C103
    （2）证明：Ank+kAnk-1=An+1k．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在二项式定理这节教材中有这样一个性质：Cn0+Cn1+Cn2+Cn3+…Cnn=2n，n∈N
    （1）计算1•C30+2•C31+3•C32+4•C33的值方法如下：
    设S=1•C30+2•C31+3•C32+4•C33又S=4•C33+3•C32+2•C31+1•C30
    相加得2S=5•C30+5•C31+5•C32+5•C33即2S=5•23
    所以2S=5•22=20利用类似方法求值：1•C20+2•C21+3•C22，1•C40+2•C41+3•C42+4•C43+5•C44
    （2）将（1）的情况推广到一般的结论，并给予证明
    （3）设Sn是首项为a1，公比为q的等比数列{an}的前n项的和，求S1Cn0+S2Cn1+S3Cn2+S4Cn3+…+Sn+1Cnn，n∈N．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （1）计算：C33+C43+C53+…+C103
    （2）证明：Ank+kAnk-1=An+1k．

    查看答案和解析>>

    科目：高中数学 来源：陕西省期末题 题型：计算题

    （1）计算：C33+C43+C53+…+C103
    （2）证明：Ank+kAnk﹣1=An+1k．

    查看答案和解析>>

    同步练习册答案