
【题目】已知数列{an}的各项均为正数,a1=1,前n项和为Sn , 且an+12﹣nλ2﹣1=2λSn , λ为正常数.
(1)求数列{an}的通项公式;
(2)记bn= ![]() ,Cn=
,Cn= ![]() +
+ ![]() (k,n∈N*,k≥2n+2). 求证:
(k,n∈N*,k≥2n+2). 求证:
①bn<bn+1;
②Cn>Cn+1 .
【答案】
(1)解:∵a2n+1﹣nλ2﹣1=2λSn,λ为正常数.∴n≥2时, ![]() ﹣(n﹣1)λ2﹣1=2λSn﹣1.
﹣(n﹣1)λ2﹣1=2λSn﹣1.
∴a2n+1﹣nλ2﹣ ![]() +(n﹣1)λ2=2λan.化为:an+1﹣an=λ.
+(n﹣1)λ2=2λan.化为:an+1﹣an=λ.
n=1时, ![]() ﹣1=2λ,解得a2=λ+1,因此a2﹣a1=λ.
﹣1=2λ,解得a2=λ+1,因此a2﹣a1=λ.
∴数列{an}是等差数列,公差为λ.
∴an=1+λ(n﹣1)
(2)证明:①由(1)可得:Sn= ![]() .
.
∴bn= ![]() =
= ![]() =
= ![]() .
.
bn+1﹣bn= ![]() =
= ![]() >0.
>0.
∴bn+1>bn.
②∵Cn= ![]() +
+ ![]() ,(k,n∈N*,k≥2n+2).
,(k,n∈N*,k≥2n+2).
∴Cn+1﹣Cn= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]()
= ![]() +
+ ![]()
= ![]() ﹣
﹣ ![]() .
.
∵k≥2n+2,∴n+1<k﹣n,n<k﹣n﹣1.
由an>0,∴0<Sn<Sk﹣n﹣1,∴ ![]() .
.
又0<bn+1<bk﹣n,∴ ![]() <
< ![]() ,
,
∴Cn+1﹣Cn<0.∴Cn>Cn+1
【解析】(1)a2n+1﹣nλ2﹣1=2λSn , λ为正常数.可得:n≥2时, ![]() ﹣(n﹣1)λ2﹣1=2λSn﹣1 . 相减化为:an+1﹣an=λ.n=1时,
﹣(n﹣1)λ2﹣1=2λSn﹣1 . 相减化为:an+1﹣an=λ.n=1时, ![]() ﹣1=2λ,解得a2=λ+1,因此a2﹣a1=λ.利用等差数列的通项公式可得:an=1+λ(n﹣1).(2)①由(1)可得:Sn=
﹣1=2λ,解得a2=λ+1,因此a2﹣a1=λ.利用等差数列的通项公式可得:an=1+λ(n﹣1).(2)①由(1)可得:Sn= ![]() .可得bn=
.可得bn= ![]() =
= ![]() ,作差bn+1﹣bn , 化简即可得出.②Cn=
,作差bn+1﹣bn , 化简即可得出.②Cn= ![]() +
+ ![]() ,(k,n∈N*,k≥2n+2).作差Cn+1﹣Cn=
,(k,n∈N*,k≥2n+2).作差Cn+1﹣Cn= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() .利用其单调性即可得出.
.利用其单调性即可得出.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系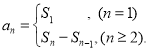 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】如图,等边三角形![]() 的中线
的中线![]() 与中位线
与中位线![]() 相交于
相交于![]() ,已知
,已知![]() 是
是![]() 绕
绕![]() 旋转过程中的一个图形,下列命题中,错误的是
旋转过程中的一个图形,下列命题中,错误的是

A. 恒有![]() ⊥
⊥![]()
B. 异面直线![]() 与
与![]() 不可能垂直
不可能垂直
C. 恒有平面![]() ⊥平面
⊥平面![]()
D. 动点![]() 在平面
在平面![]() 上的射影在线段
上的射影在线段![]() 上
上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() .
.
(1)若直线![]() 与直线
与直线![]() 平行,求实数
平行,求实数![]() 的值;
的值;
(2)若![]() ,
, ![]() ,点
,点![]() 在直线
在直线![]() 上,已知
上,已知![]() 的中点在
的中点在![]() 轴上,求点
轴上,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据两直线平行,对应方向向量共线,列方程即可求出![]() 的值;(2)根据
的值;(2)根据![]() 时,直线
时,直线![]() 的方程设出点
的方程设出点![]() 的坐标,由此求出
的坐标,由此求出![]() 的中点坐标,再由中点在
的中点坐标,再由中点在![]() 轴上求出点
轴上求出点![]() 的坐标.
的坐标.
试题解析:(1)∵直线![]() 与直线
与直线![]() 平行,
平行,
∴![]() ,
,
∴![]() ,经检验知,满足题意.
,经检验知,满足题意.
(2)由题意可知: ![]() ,
,
设![]() ,则
,则![]() 的中点为
的中点为![]() ,
,
∵![]() 的中点在
的中点在![]() 轴上,∴
轴上,∴![]() ,
,
∴![]() .
.
【题型】解答题
【结束】
16
【题目】在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,-4).
(1)求BC边上的中线所在直线的方程;
(2)求BC边上的高所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是公比大于1的等比数列,Sn为数列{an}的前n项和,已知S3=7,
且a1+3,3a2,a3+4构成等差数列.
(1)求数列{an}的通项;
(2)令![]() ,n=1,2,…,求数列{bn}的前n项和Tn .
,n=1,2,…,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆 ![]() +
+ ![]() =1(a>b>0)的离心率为e,D为右准线上一点.
=1(a>b>0)的离心率为e,D为右准线上一点.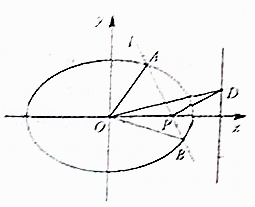
(1)若e= ![]() ,点D的横坐标为4,求椭圆的方程;
,点D的横坐标为4,求椭圆的方程;
(2)设斜率存在的直线l经过点P( ![]() ,0),且与椭圆交于A,B两点.若
,0),且与椭圆交于A,B两点.若 ![]() +
+ ![]() =
= ![]() ,DP⊥l,求椭圆离心率e.
,DP⊥l,求椭圆离心率e.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量 ![]() 的取值为不大于
的取值为不大于 ![]() 的非负整数值,它的分布列为:
的非负整数值,它的分布列为:
| 0 | 1 | 2 |
| n |
|
|
|
|
|
|
其中 ![]() (
( ![]() )满足:
)满足: ![]() ,且
,且 ![]() .
.
定义由 ![]() 生成的函数
生成的函数 ![]() ,令
,令 ![]() .
.
(I)若由 ![]() 生成的函数
生成的函数 ![]() ,求
,求 ![]() 的值;
的值;
(II)求证:随机变量 ![]() 的数学期望
的数学期望 ![]() ,
, ![]() 的方差
的方差 ![]() ;
;
( ![]() )
)
(Ⅲ)现投掷一枚骰子两次,随机变量 ![]() 表示两次掷出的点数之和,此时由
表示两次掷出的点数之和,此时由 ![]() 生成的函数记为
生成的函数记为 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某社区中学生的课外活动,对该社区的100名中学生进行了调研,随机抽取了若干名,年龄全部介于13与18之间,将年龄按如下方式分成五组:第一组![]() ;第二组
;第二组![]() ;第五组
;第五组![]() .按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三个组的频率之比为
.按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三个组的频率之比为![]() ,且第二组的频数为4.
,且第二组的频数为4.
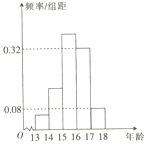
(1)试估计这100名中学生中年龄在![]() 内的人数;
内的人数;
(2)求调研中随机抽取的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρ2(1+3sin2θ)=4,曲线C2: ![]() (θ为参数).
(θ为参数).
(Ⅰ)求曲线C1的直角坐标方程和C2的普通方程;
(Ⅱ)极坐标系中两点A(ρ1 , θ0),B(ρ2 , θ0+ ![]() )都在曲线C1上,求
)都在曲线C1上,求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=cos(2x+ ![]() )+2cos2x,x∈R.
)+2cos2x,x∈R.
(1)求函数f(x)的最小正周期和单调增区间;
(2)将函数f(x)的图象向右平移 ![]() 个单位长度后得到函数g(x)的图象,求函数g(x)在区间
个单位长度后得到函数g(x)的图象,求函数g(x)在区间 ![]() 上的值域.
上的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com