
| | 采桑 | 不采桑 | 合计 |
| 患者人数 | 18 | 12 | |
| 健康人数 | 5 | 78 | |
| 合计 | | | |
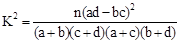
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
 =bx+a;
=bx+a;
| n-2 | 1 | 2 | 3 | 4 |
| 小概率0.05 | 0.997 | 0.950 | 0.878 | 0.811 |
| 小概率0.01 | 1.000 | 0.990 | 0.959 | 0.917 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,
,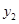 ,
, ,
, 随变量
随变量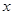 变化的数据如下表:
变化的数据如下表: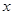 | 0 | 5 | 10 | 15 | 20 | 25 |
 | 5 | 130 | 505 | 1130 | 2005 | 3130 |
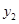 | 5 | 94.478 | 1785.2 | 33733 | 6.37 | 1.2 |
 | 5 | 30 | 55 | 80 | 105 | 130 |
 | 5 | 2.3107 | 1.4295 | 1.11407 | 1.0461 | 1.0151 |
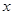 呈指数型函数变化的变量是( )
呈指数型函数变化的变量是( ) B.
B.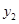 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
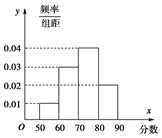
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.7,5,8 | B.9,5,6 | C.6,5,9 | D.8,5,7 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | 硕士 | 博士 | 合计 |
| 男 | 162 | 27 | 189 |
| 女 | 143 | 8 | 151 |
| 合计 | 305 | 35 | 340 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com