[题目]若以直角坐标系xOy的O为极点.Ox为极轴.选择相同的长度单位建立极坐标系.得曲线C的极坐标方程是ρ= ．(1)将曲线C的极坐标方程化为直角坐标方程.并指出曲线是什么曲线,(2)若直线l的参数方程为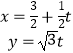当直线l与曲线C相交于A.B两点.求|

精英家教网 > 高中数学 > 题目详情

【题目】若以直角坐标系xOy的O为极点，Ox为极轴，选择相同的长度单位建立极坐标系，得曲线C的极坐标方程是ρ= ．
（1）将曲线C的极坐标方程化为直角坐标方程，并指出曲线是什么曲线；
（2）若直线l的参数方程为（t为参数）当直线l与曲线C相交于A，B两点，求| |

【答案】
（1）解：∵ρ= ，∴ρ2sin2θ=6ρcosθ，

∴曲线C的直角坐标方程为y2=6x．曲线为以（，0）为焦点，开口向右的抛物线．

（2）解：直线l的参数方程可化为，代入y2=6x得t2﹣4t﹣12=0．

解得t1=﹣2，t2=6．

∴| |=|t1﹣t2|=8

【解析】（1）将极坐标方程两边同乘ρ，去分母即可得到直角坐标方程；（2）写出直线l参数方程的标准形式，代入曲线C的普通方程，根据参数的几何意义得出|AB|．

练习册系列答案

一通百通小学毕业升学模拟测试卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，在平面直角坐标系xOy中，以x轴正半轴为始边作锐角α，其终边与单位圆交于点A．以OA为始边作锐角β，其终边与单位圆交于点B，AB= ．
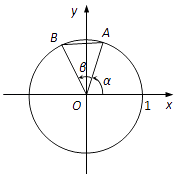
（1）求cosβ的值；
（2）若点A的横坐标为，求点B的坐标．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数，.

（1）问：能否为偶函数？请说明理由；

（2）总存在一个区间，当时，对任意的实数，方程无解，当时，存在实数，方程有解，求区间.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某城市户居民的月平均用电量（单位：度），以，，，，，，分组的频率分布直方图如图．

（1）求直方图中的值；

（2）求月平均用电量的众数和中位数；

（3）在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取户居民，则月平均用电量在的用户中应抽取多少户？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】下列说法正确的是（）
A.“sinα= ”是“cos2α= ”的必要不充分条件
B.已知命题p：?x∈R，使2x＞3x；命题q：?x∈（0，+∞），都有＜，则p∧（￢q）是真命题
C.命题“若xy=0，则x=0或y=0”的否命题是“若xy≠0，则x≠0或y≠0”
D.从匀速传递的生产流水线上，质检员每隔5分钟从中抽取一件产品进行某项指标检测，这是分成抽样