
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点
的中点
(1)证明:![]() ;
;
(2)若![]() 为棱
为棱![]() 上一点,满足
上一点,满足![]() ,求锐二面角
,求锐二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见详解;(2)![]()
【解析】
(1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法证明![]() ;
;
(2)设![]() ,由
,由![]() ,求出
,求出![]() ,求出平面ABF的法向量和平面ABP的法向量,利用向量法能求出二面角
,求出平面ABF的法向量和平面ABP的法向量,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
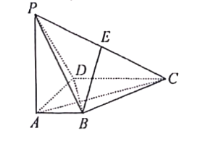
证明:(1)∵在四棱锥PABCD中,PA⊥底面ABCD,AD⊥AB,
AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
∴以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
B(1,0,0),P(0,0,2),C(2,2,0),E(1,1,1),D(0,2,0),![]() ,
,![]() ,
,![]() ,
,
∴![]() ;
;
(2)∵F为棱PC上一点,满足![]() ,
,
∴设![]() ,
,![]() ,
,
则![]() ,
,
![]() ,
,
∵![]() ,
,![]() ,
,
解得![]() ,
,![]() ,
,
设平面ABF的法向量![]() ,
,
则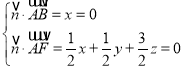 ,取
,取,得
![]() ,
,
平面ABP的一个法向量![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,
,
则![]() ,
,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,且椭圆
,且椭圆![]() 的离心率为
的离心率为![]() ,过
,过![]() 作
作![]() 轴的垂线与椭圆
轴的垂线与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,动点
,动点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)记椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,且直线
,且直线![]() 的斜率分别与直线
的斜率分别与直线![]() (
(![]() 为坐标原点)的斜率相同,动点
为坐标原点)的斜率相同,动点![]() 不与
不与![]() 重合,求
重合,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地环保部门跟踪调查一种有害昆虫的数量.根据调查数据,该昆虫的数量![]() (万只)与时间
(万只)与时间![]() (年)(其中
(年)(其中![]() )的关系为
)的关系为![]() .为有效控制有害昆虫数量、保护生态环境,环保部门通过实时监控比值
.为有效控制有害昆虫数量、保护生态环境,环保部门通过实时监控比值![]() (其中
(其中![]() 为常数,且
为常数,且![]() )来进行生态环境分析.
)来进行生态环境分析.
(1)当![]() 时,求比值
时,求比值![]() 取最小值时
取最小值时![]() 的值;
的值;
(2)经过调查,环保部门发现:当比值![]() 不超过
不超过![]() 时不需要进行环境防护.为确保恰好3年不需要进行保护,求实数
时不需要进行环境防护.为确保恰好3年不需要进行保护,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数的底,
为自然对数的底, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C与圆C1:5x2+5y2﹣mx﹣16y+32=0外切于点P(![]() ),且与y轴相切.
),且与y轴相切.
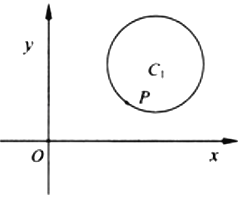
(1)求圆C的方程
(2)过点O作直线l1,l2分别交圆C于A、B两点,若l1,l2斜率之积为﹣2,求△ABC面积S的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有9只球,其中标有数字1,2,3,4的小球各2个,标数字5的小球有1个.从袋中任取3个小球,每个小球被取出的可能性都相等,用![]() 表示取出的3个小球上的最大数字.
表示取出的3个小球上的最大数字.
(1)求取出的3个小球上的数字互不相同的概率;
(2)求随机变量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车的投放,方便了市民短途出行,被誉为中国“新四大发明”之一.某市为研究单车用户与年龄的相关程度,随机调查了100位成人市民,统计数据如下:
不小于40岁 | 小于40岁 | 合计 | |
单车用户 | 12 | y | m |
非单车用户 | x | 32 | 70 |
合计 | n | 50 | 100 |
(1)求出列联表中字母x、y、m、n的值;
(2)①从此样本中,对单车用户按年龄采取分层抽样的方法抽出5人进行深入调研,其中不小于40岁的人应抽多少人?
②从独立性检验角度分析,能否有![]() 以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关.
以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关.
下面临界值表供参考:
P( | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
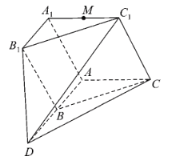
【题目】如图,已知平面![]() 平面
平面![]() ,B为线段
,B为线段![]() 的中点,
的中点,![]() ,四边形
,四边形![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,M为棱
,M为棱![]() 的中点.
的中点.
(1)若N为线段![]() 上的点,且直线
上的点,且直线![]() 平面
平面![]() ,试确定点N的位置;
,试确定点N的位置;
(2)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com