
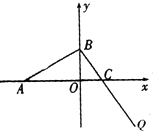
 如图,已知A(-3,0),B、C两点分别在y轴和x轴上运动,并且满足
如图,已知A(-3,0),B、C两点分别在y轴和x轴上运动,并且满足| AB |
| BQ |
| BC |
| 1 |
| 2 |
| CQ |
| AB |
| BQ |
| BC |
| 1 |
| 2 |
| CQ |
| AB |
| BC |
| CQ |
| BQ |
| AB |
| BQ |
| BC |
| 1 |
| 2 |
| CQ |
|
|
| 4-6k2 |
| k2 |
| y1 |
| x1-3 |
| y2 |
| x2-3 |
| y1(x2-3)+y2(x1-3) |
| (x1-3)(x2-3) |
| k(x1+3)(x2-3)+k(x2+3)(x1-3) |
| x1x2-3(x1+x2)+9 |
| 2k(x1x2-9) |
| x1x2-3(x1+x2)-9 |
| 2k(9-9) |
| x1x2-3(x1+x2)-9 |


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
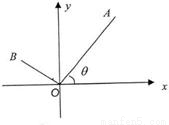
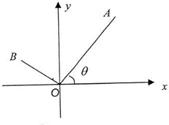 如图,已知A(3,4),点O为坐标原点,点B在第二象限,且|OB|=3,记∠AOx=θ.
如图,已知A(3,4),点O为坐标原点,点B在第二象限,且|OB|=3,记∠AOx=θ.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
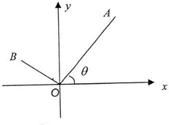
查看答案和解析>>
科目:高中数学 来源:2010-2011学年黑龙江省绥化市庆安三中高三(上)期中数学试卷(文科)(解析版) 题型:解答题
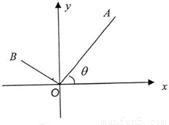
查看答案和解析>>
科目:高中数学 来源:2010年黑龙江省高考数学模拟试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com