
【题目】设数列{an}的前n项和为Sn , a1=10,an+1=9Sn+10.
(1)求证:{lgan}是等差数列;
(2)设 ![]() 对所有的n∈N*都成立的最大正整数m的值.
对所有的n∈N*都成立的最大正整数m的值.
【答案】
(1)证明:依题意, ![]() ,
,
当n≥2时,an=9Sn﹣1+10①又an+1=9Sn+10②
②﹣①整理得: ![]() 为等比数列,
为等比数列,
且an=a1qn﹣1=10n,∴lgan=n∴lgan+1﹣lgan=(n+1)﹣n=1,
即{lgan}n∈N*是等差数列.
(2)解:由(1)知, ![]()
= ![]() ∴
∴ ![]() ,
,
依题意有 ![]() ,
,
故所求最大正整数m的值为5.
【解析】(1)依题意可求得a2的值,进而求得 ![]() 的值,进而看当n≥2时,根据an=Sn﹣Sn﹣1求得
的值,进而看当n≥2时,根据an=Sn﹣Sn﹣1求得 ![]() 判断出数列为等比数列,进而根据等比数列的性质求得an , 进而分别表示出lgan和lgan+1 , 根据lgan+1﹣lgan=1,判断出lgan}n∈N*是等差数列.(2)根据(1)中求得an利用裂项法求得Tn , 进而根据3﹣
判断出数列为等比数列,进而根据等比数列的性质求得an , 进而分别表示出lgan和lgan+1 , 根据lgan+1﹣lgan=1,判断出lgan}n∈N*是等差数列.(2)根据(1)中求得an利用裂项法求得Tn , 进而根据3﹣ ![]() ≥
≥ ![]() ,进而根据
,进而根据 ![]() 求得m的范围.判断出m的最大正整数.
求得m的范围.判断出m的最大正整数.
【考点精析】利用等差关系的确定和数列的前n项和对题目进行判断即可得到答案,需要熟知如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列;数列{an}的前n项和sn与通项an的关系
)那么这个数列就叫做等差数列;数列{an}的前n项和sn与通项an的关系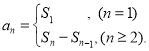 .
.


科目:高中数学 来源: 题型:
【题目】如图四边形ABCD为梯形,AD∥BC,∠ABC=90°,AD=2,AB=4,BC=5,图中阴影部分(梯形剪去一个扇形)绕AB旋转一周形成一个旋转体.
(1)求该旋转体的表面积;
(2)求该旋转体的体积. 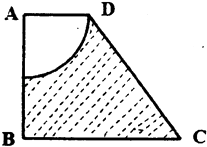
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个,生产一个卫兵需5分钟,生产一个骑兵需7分钟,生产一个伞兵需4分钟,已知总生产时间不超过10小时.若生产一个卫兵可获利润5元,生产一个骑兵可获利润6元,生产一个伞兵可获利润3元.
(1)用每天生产的卫兵个数x与骑兵个数y表示每天的利润W(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取40中学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段: ![]() ,
, ![]() ,…,
,…, ![]() 所得到如图所示的频率分布直方图.
所得到如图所示的频率分布直方图.

(1)求图中实数![]() 的值;
的值;
(2)若该校高一年级共有640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在![]() 与
与![]() 两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a,b是函数f(x)=x2﹣px+q(p>0,q>0)的两个不同的零点,且a,b,﹣2这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p+q的值等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,M为AB的中点,点F在PA上,且2PF=FA. 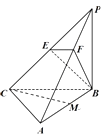
(1)求证:BE⊥平面PAC;
(2)求证:CM∥平面BEF;
(3)求平面ABC与平面BEF所成的二面角的平面角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA= ![]() acosB.
acosB.
(1)求角B的大小;
(2)若b=3,sinC=2sinA,分别求a和c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com