
在△ABC中,内角A,B,C所对的边分别是a,b,c,已知a=2,c= ,
, .
.
(1)求sinC和b的值;
(2)求cos 的值.
的值.
(1)sinC=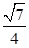 ,b=1;(2)
,b=1;(2)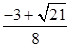 .
.
解析试题分析:(1)△ABC中,利用同角三角函数的基本关系求出sinA,再由正弦定理求出sinC,再由余弦定理求得b=1;(2)利用二倍角公式求得cos2A的值,由此求得sin2A,再由两角和的余弦公式求出cos(2A+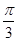 )=cos2Acos
)=cos2Acos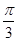 -sin2Asin
-sin2Asin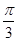 的值.
的值.
解:(1)在△ABC中,由cosA=- ,可得sinA=
,可得sinA=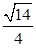 ,又由
,又由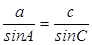 及a=2,c=
及a=2,c=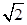 ,可得sinC=
,可得sinC=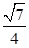 .
.
由a2=b2+c2-2bccosA,得b2+b-2=0,
因为b>0,故解得b=1.所以sinC=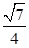 ,b=1 5分
,b=1 5分
(2)由cosA=- ,sinA=
,sinA=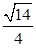 ,
,
得cos2A=2cos2A-1=-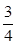 ,
,
sin2A=2sinAcosA=-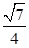 .
.
所以,cos =cos2Acos
=cos2Acos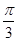 -sin2Asin
-sin2Asin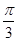 =
=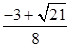 ..............10分
..............10分
考点:1.解三角形;2.三角函数中的恒等变换应用.


科目:高中数学 来源: 题型:解答题
如图,小岛A的周围3.8海里内有暗礁.一艘渔船从B地出发由西向东航行,观测到小岛A在北偏东75°,继续航行8海里到达C处,观测到小岛A在北偏东60°.若此船不改变航向继续前进,有没有触礁的危险?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com