练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．函数f（x）=x3+ax2+（a+6）x+1在R上存在极值，则实数a的取值范围（　　）
    A．-3≤a≤6B．a≥6或a≤-3C．-3＜a＜6D．a＞6或a＜-3

    分析 求出函数的导数，由题意得函数的导数在R上至少有一个零点，主要不能有两个相等的零点，即可求出实数a的取值范围．

    解答 解：∵f（x）=x3+ax2+（a+6）x+1，
    ∴f′（x）=3x2+2ax+a+6，
    ∵函数f（x）=x3+ax2+（a+6）x+1在R上存在极值，
    ∴函数f（x）=x3+ax2+（a+6）x+1在R上不是单调函数
    ∴f′（x）=3x2+2ax+a+6=0有两个不等的根，
    即△=4a2-12a-72＞0，
    解得a＜-3，或a＞6，
    故选：D．

    点评 本题考查了利用导数研究三次多项式函数的单调性，从而求参数a的取值范围，属于中档题，解题时应该注意导函数等于0的等根的情形，以免出现只一个零点的误解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    1．在等差数列{an}中，a1=2，S3=9．
    （1）求{an}的通项公式an；
    （2）求{2${\;}^{{a}_{n}}$}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=x2+alnx．
    （1）当a=-2e时，求函数f（x）的极值；
    （2）若函数g（x）=f（x）+$\frac{2}{x}$在[1，2]上是单调增函数，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．如图是某校十大歌手比赛上，七位评委为某同学打出的分数的茎叶图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（　　）
    A．85，4.84B．85，1.6C．86，1.6D．86，4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．若不等式x2-2ax+a＞0对一切实数x∈R恒成立，则关于t的不等式loga（t2+2t-2）＞0的解集为（　　）
    A．（-3，1）B．$（-1+\sqrt{3}，1）∪（-3，-1-\sqrt{3}）$C．$（-1-\sqrt{3}，-1+\sqrt{3}）$D．$（-∞，-1-\sqrt{3}）∪（-1+\sqrt{3}，+∞）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知Sn是等差数列{an}的前n项和，a4=7，S8=64、
    （I）求数列{an}的通项公式
    （II）设bn=$\frac{1}{{a}_{n}{a}_{n+1}}$，求数列{bn}的前100项的和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

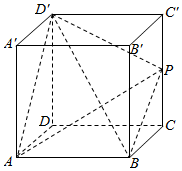    3．在棱长为4的正方体ABCD-A′B′C′D′中，点P在棱CC′上，且CC′=2CP．
    （1）求直线AA′与平面APD′所成角的正弦值；
    （2）求二面角A-D′P-B的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．如图，四棱锥P-ABCD中，ABCD是边长为2的菱形，且∠DAB=60°，PC=4，PA=2，E是PA的中点，平面PAC⊥平面ABCD．
    （Ⅰ）求证：PC∥平面BDE；
    （Ⅱ）求二面角P-BD-E的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．如图，已知⊙A和⊙B的公共弦CD与AB相交于点E，CB与⊙A相切，⊙B半径为2，AE=3．
    （Ⅰ）求弦CD的长；
    （Ⅱ）⊙B与线段AB相交于点F，延长CF与⊙A相交于点G，求CG的长．

    查看答案和解析>>

    同步练习册答案