
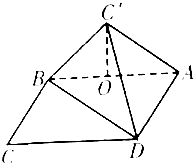
 如图.在矩形ABCD中.AB=3 $\sqrt{3}$,BC=3,沿对角线BD把△BCD折起.使C移到C′.且C′在面ABC内的射影O恰好落在AB上.
如图.在矩形ABCD中.AB=3 $\sqrt{3}$,BC=3,沿对角线BD把△BCD折起.使C移到C′.且C′在面ABC内的射影O恰好落在AB上.分析 (1)推导出AD⊥AB,AD⊥C′O,从而AD⊥平面AC′O,由此能证明AD⊥BC′.
(2)推导出BP⊥DC′,AD⊥C′O,C′B⊥AD,从而BC′⊥平面ADC′,从而能证明平面DBC′⊥平面ADC′.
(3)由C′O⊥平面ABD,得到三棱锥C′-ABD的体积V=$\frac{1}{3}×{S}_{△ABD}×{C}^{'}O$,由此能求出结果.
解答 证明:(1)∵在矩形ABCD,∴AD⊥AB,
∵C′在面ABC内的射影O恰好落在AB上,
∴C′O⊥平面ABCD,AD?平面ABCD,
∴AD⊥C′O,
∵AB∩C′O=O,∴AD⊥平面AC′O,
∵BC′?平面AC′O,∴AD⊥BC′.
(2):∵在矩形ABCD中,BC⊥CD,AB⊥AD,
∴折起后,BP⊥DC′,
∵沿对角线BD把△BCD折起,使点C移到点C′,
且点C′在面ABD内的射影O恰好落在AB上,
∴C′O⊥平面ABD,又AD?平面ABD,∴AD⊥C′O,
又AB∩C′O=O,∴AD⊥平面C′AB,
又C′B?平面C′AB,∴C′B⊥AD,
∵AD∩DC′=D,∴BC′⊥平面ADC′,
又BC′?平面DBC′,∴平面DBC′⊥平面ADC′.
解:(3)∵C′O⊥平面ABCD,∴C′O⊥平面ABD,
∵在矩形ABCD中,AB=3$\sqrt{3}$,BC=3,
∴BC′=AD=3,C′D=3$\sqrt{3}$,∴C′A=$\sqrt{{C}^{'}{D}^{2}-A{D}^{2}}$=3$\sqrt{2}$,
∴C′O=$\frac{B{C}^{'}•{C}^{'}A}{AB}$=$\sqrt{6}$,
∴S△ABD=$\frac{1}{2}×3\sqrt{3}×3=\frac{9\sqrt{3}}{2}$,
∴三棱锥C′-ABD的体积V=$\frac{1}{3}×{S}_{△ABD}×{C}^{'}O$=$\frac{1}{3}×\frac{9\sqrt{3}}{2}×\sqrt{6}$=$\frac{9\sqrt{2}}{2}$.
点评 本题考查线线垂直的证明,考查面面垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | -1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>a>b | C. | b>a>c | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | [$\frac{1}{2}$,2] | C. | [$\frac{1}{2}$,1] | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [6-2$\sqrt{6}$,9] | B. | [6-2$\sqrt{6}$,11] | C. | [6+2$\sqrt{6}$,9] | D. | [6+2$\sqrt{6}$,11] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com