
【题目】如图所示,用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥,放在水平桌面上,被一阵风吹倒.
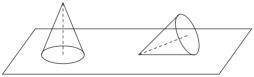
(1)求该圆锥的表面积![]() 和体积
和体积![]() ;
;
(2)求该圆锥被吹倒后,其最高点到桌面的距离![]() .
.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,有下列四个结论:
①AP与CM是异面直线;②AP,CM,DD1相交于一点;③MN∥BD1;
④MN∥平面BB1D1D.
其中所有正确结论的编号是( )

A.①④B.②④C.①④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“家校连心,立德树人——重温爱国故事,弘扬爱国主义精神社会课堂”活动中,王老师组建了一个微信群,群的成员由学生、家长、老师和讲解员共同组成.已知该微信群中男学生人数多于女生人数,女学生人数多于家长人数,家长人数多于教师人数,教师人数多于讲解员人数,讲解员人数的两倍多于男生人数.若把这5类人群的人数作为一组数据,当该微信群总人数取最小值时,这组数据的中位数是( )
A.5B.6C.7D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着全球石油资源紧张、大气污染日益严重和电池技术的提高,电动汽车已被世界公认为21世纪汽车工业改造和发展的主要方向.为了降低对大气的污染和能源的消耗,某品牌汽车制造商研发了两款电动汽车车型![]() 和车型
和车型![]() ,并在黄金周期间同时投放市场.为了了解这两款车型在黄金周的销售情况,制造商随机调查了5家汽车
,并在黄金周期间同时投放市场.为了了解这两款车型在黄金周的销售情况,制造商随机调查了5家汽车![]() 店的销量(单位:台),得到下表:
店的销量(单位:台),得到下表:
| 甲 | 乙 | 丙 | 丁 | 戊 |
车型 | 6 | 6 | 13 | 8 | 11 |
车型 | 12 | 9 | 13 | 6 | 4 |
(1)若从甲、乙两家![]() 店销售出的电动汽车中分别各自随机抽取1台电动汽车作满意度调查,求抽取的2台电动汽车中至少有1台是车型
店销售出的电动汽车中分别各自随机抽取1台电动汽车作满意度调查,求抽取的2台电动汽车中至少有1台是车型![]() 的概率;
的概率;
(2)现从这5家汽车![]() 店中任选3家举行促销活动,用
店中任选3家举行促销活动,用![]() 表示其中车型
表示其中车型![]() 销量超过车型
销量超过车型![]() 销量的
销量的![]() 店的个数,求随机变量
店的个数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,设
,设![]() 为线段
为线段![]() 的中点.则在
的中点.则在![]() 翻折过程中,给出如下结论:
翻折过程中,给出如下结论:
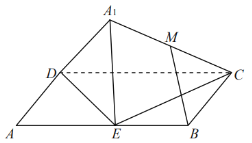
①当![]() 不在平面
不在平面![]() 内时,
内时,![]() 平面
平面![]() ;
;
②存在某个位置,使得![]() ;
;
③线段![]() 的长是定值;
的长是定值;
④当三棱锥![]() 体积最大时,其外接球的表面积为
体积最大时,其外接球的表面积为![]() .
.
其中,所有正确结论的序号是______.(请将所有正确结论的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为坐标原点,动点
为坐标原点,动点![]() 在圆
在圆![]() 上,过
上,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 满足
满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 上的点
上的点![]() 满足
满足![]() .过点
.过点![]() 作直线
作直线![]() 垂直于线段
垂直于线段![]() 交
交![]() 于点
于点![]() .
.
(ⅰ)证明:![]() 恒过定点;
恒过定点;
(ⅱ)设线段![]() 交
交![]() 于点
于点![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的五面体中,![]() 是正方形,
是正方形,![]() 是等腰梯形,且平面
是等腰梯形,且平面![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)![]() 为线段
为线段![]() 的中点,
的中点,![]() 在线段
在线段![]() 上,记
上,记![]() ,
,![]() 是线段
是线段![]() 上的动点. 当
上的动点. 当![]() 为何值时,三棱锥
为何值时,三棱锥![]() 的体积为定值?证明此时二面角
的体积为定值?证明此时二面角![]() 为定值,并求出其余弦值.
为定值,并求出其余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com