
【题目】为了解学生对“两个一百年”奋斗目标、实现中华民族伟大复兴中国梦的“关注度”(单位:天),某中学团委组织学生在十字路口采用随机抽样的方法抽取了80名青年学生(其中男女人数各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组青年学生的月“关注度”分为6组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.

(1)求![]() 的值;
的值;
(2)现从“关注度”在![]() 的男生与女生中选取3人,设这3人来自男生的人数为
的男生与女生中选取3人,设这3人来自男生的人数为![]() ,求
,求![]() 的分布列与期望;
的分布列与期望;
(3)在抽取的80名青年学生中,从月“关注度”不少于25天的人中随机抽取2人,求至少抽取到1名女生的概率.
【答案】(1)0.05;(2)答案见解析;(3) ![]() .
.
【解析】试题分析: ![]() 由频率分布的性质易得
由频率分布的性质易得![]() 的值;
的值;
![]() 计算出男生与女生的人数,得出
计算出男生与女生的人数,得出![]() 的取值可以为1,2,3,然后列分布表求期望(3)抽取到1名女生分为1名女生1名男生与2名女生两种情况,利用古典概率公式求解即可
的取值可以为1,2,3,然后列分布表求期望(3)抽取到1名女生分为1名女生1名男生与2名女生两种情况,利用古典概率公式求解即可
解析:(1)![]() .
.
(2)从频率分布直方图可知在![]() 内的男生人数为
内的男生人数为![]() 人,女生人数为
人,女生人数为![]() 人,男女生共6人,因此
人,男女生共6人,因此![]() 的取值可以为1,2,3,
的取值可以为1,2,3,
故![]() ,
, ![]() ,
, ![]() .
.
所以![]() 的分布列为
的分布列为
| 1 | 2 | 3 |
|
|
|
|
数学期望![]() .
.
(3)记“在抽取的80名青年学生中,从月“关注度”不少于25天的人中随机抽取2人,至少抽到1名女生”为事件![]() ,
,
在抽取的女生中,月“关注度”不少于25天即在![]() 内的人数为2,在抽取的男生中,月“关注度”不少于25天即在
内的人数为2,在抽取的男生中,月“关注度”不少于25天即在![]() 内的人数为4,
内的人数为4,
则在抽取的80名学生中,共有6人月“关注度”不少于25天,从中随机抽取2人,所有可能的结果有![]() 种,
种,
而事件![]() 包含的结果有
包含的结果有![]() 种,
种,
所以![]() .
.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】某货轮匀速行驶在相距300海里的甲、乙两地间运输货物,运输成本由燃料费用和其它费用组成,已知该货轮每小时的燃料费用与其航行速度的平方成正比(比例系数为0.5),其它费用为每小时800元,且该货轮的最大航行速度为50海里/小时.
(1)请将从甲地到乙地的运输成本y(元)表示为航行速度x(海里/小时)的函数;
(2)要使从甲地到乙地的运输成本最少,该货轮应以多大的航行速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣
x3﹣ ![]() (m+3)x2+(m+6)x,x∈R.(其中m为常数)
(m+3)x2+(m+6)x,x∈R.(其中m为常数)
(1)当m=4时,求函数的极值点和极值;
(2)若函数y=f(x)在区间(0,+∞)上有两个极值点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x+ ![]() )+1,△ABC中,角A、B、C的对边分别是a、b、c.
)+1,△ABC中,角A、B、C的对边分别是a、b、c.
(1)若角A、B、C成等差数列,求f(B)的值;
(2)若f( ![]() ﹣
﹣ ![]() )=
)= ![]() ,边a、b、c成等比数列,△ABC的面积S=
,边a、b、c成等比数列,△ABC的面积S= ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两直线l1:x+8y+7=0和l2:2x+y﹣1=0.
(1)求l1与l2交点坐标;
(2)求过l1与l2交点且与直线x+y+1=0平行的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点P(0,﹣1)是椭圆C1: ![]() =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1 , l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1 , l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D. 
(1)求椭圆C1的方程;
(2)求△ABD面积的最大值时直线l1的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别是焦距为
分别是焦距为![]() 的椭圆
的椭圆![]() 的左、右顶点,
的左、右顶点, ![]() 为椭圆
为椭圆![]() 上非顶点的点,直
上非顶点的点,直![]() 线的斜率分别为
线的斜率分别为![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() (与
(与![]() 轴不重合)过点
轴不重合)过点![]() 且与椭圆
且与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 与
与![]() 交于点
交于点![]() ,试求
,试求![]() 点的轨迹是否是垂直
点的轨迹是否是垂直![]() 轴的直线,若是,则求出
轴的直线,若是,则求出![]() 点的轨迹方程,若不是,请说明理由.
点的轨迹方程,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的![]() 分别为14,18,则输出的
分别为14,18,则输出的![]() 为( )
为( )
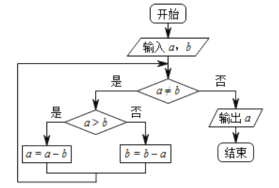
A. 0 B. 2 C. 4 D. 14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com