
【题目】某同学为研究函数![]() 的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC,点P是边BC上的一个动点,设
的性质,构造了如图所示的两个边长为1的正方形ABCD和BEFC,点P是边BC上的一个动点,设![]() ,则
,则![]() .请你参考这些信息,推知函数
.请你参考这些信息,推知函数![]() 的图象的对称轴是______;函数
的图象的对称轴是______;函数![]() 的零点的个数是______.
的零点的个数是______.

科目:高中数学 来源: 题型:
【题目】如图,点P(0,﹣1)是椭圆C1: ![]() +
+ ![]() =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1 , l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1 , l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D. 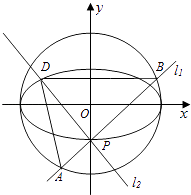
(1)求椭圆C1的方程;
(2)求△ABD面积的最大值时直线l1的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P1 , P2 , …Pn为平面α内的n个点,在平面α内的所有点中,若点P到点P1 , P2 , …Pn的距离之和最小,则称点P为P1 , P2 , …Pn的一个“中位点”,例如,线段AB上的任意点都是端点A,B的中位点,现有下列命题:
①若三个点A、B、C共线,C在线段AB上,则C是A,B,C的中位点;
②直角三角形斜边的中点是该直角三角形三个顶点的中位点;
③若四个点A、B、C、D共线,则它们的中位点存在且唯一;
④梯形对角线的交点是该梯形四个顶点的唯一中位点.
其中的真命题是(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“圆材埋壁”是《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,学会一寸,锯道长一尺,问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知道大小,用锯取锯它,锯口深一寸,锯道长一尺,问这块圆柱形木材的直径是多少?现有圆柱形木材一部分埋在墙壁中,截面如图所示,已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,则阴影部分面积约为(注:
寸,则阴影部分面积约为(注:![]() ,
,![]() ,1尺=10寸)( )
,1尺=10寸)( )

A. 6.33平方寸B. 6.35平方寸
C. 6.37平方寸D. 6.39平方寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义![]() 为n个正数
为n个正数![]() 的“均倒数”.已知正项数列{an}的前n项的“均倒数”为
的“均倒数”.已知正项数列{an}的前n项的“均倒数”为![]() .
.
(1)求数列{an}的通项公式.
(2)设数列![]() 的前n项和为
的前n项和为![]() ,若4
,若4![]() <
<![]() 对一切
对一切![]() 恒成立试求实数m的取值范围.
恒成立试求实数m的取值范围.
(3)令![]() ,问:是否存在正整数k使得
,问:是否存在正整数k使得![]() 对一切
对一切![]() 恒成立,如存在求出k值,否则说明理由.
恒成立,如存在求出k值,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某校有一块形如直角三角形ABC的空地,其中∠B为直角,AB长40米,BC长50米,现欲在此空地上建造一间健身房,其占地形状为矩形,且B为矩形的一个顶点,求该健身房的最大占地面积. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com