
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,若函数
时,若函数![]() 的导函数
的导函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,其横坐标分别为
两点,其横坐标分别为![]() ,
, ![]() ,线段
,线段![]() 的中点的横坐标为
的中点的横坐标为![]() ,且
,且![]() ,
, ![]() 恰为函数
恰为函数![]() 的零点,求证:
的零点,求证: ![]() .
.
【答案】(1)当![]() 时,
时, ![]() 在
在![]() 内单调递增;当
内单调递增;当![]() 时,
时, ![]() 在
在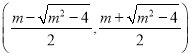 内单调递减,在
内单调递减,在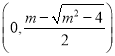 ,
, 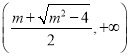 内单调递增;(2)见解析.
内单调递增;(2)见解析.
【解析】试题分析:(1)对函数求导后,利用导数与函数单调性的关系,对![]() 进行讨论可得函数单调性;(2)由函数的导函数可知,
进行讨论可得函数单调性;(2)由函数的导函数可知, ![]() 又是
又是![]() 的零点,代入相减化简得
的零点,代入相减化简得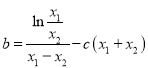 ,对
,对![]() 求导,
求导, ![]()
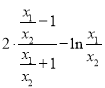 .令
.令![]() ,求得函数
,求得函数![]() .不等式得证.
.不等式得证.
试题解析:(1)由于![]() 的定义域为
的定义域为![]() ,则
,则![]() .对于方程
.对于方程![]() ,其判别式
,其判别式![]() .当
.当![]() ,即
,即![]() 时,
时, ![]() 恒成立,故
恒成立,故![]() 在
在![]() 内单调递增.当
内单调递增.当![]() ,即
,即![]() ,方程
,方程![]() 恰有两个不相等是实
恰有两个不相等是实![]() ,令
,令![]() ,得
,得![]() 或
或![]() ,此时
,此时![]() 单调递增;令
单调递增;令![]() ,得
,得![]() ,此时
,此时![]() 单调递减.
单调递减.
综上所述,当![]() 时,
时, ![]() 在
在![]() 内单调递增;当
内单调递增;当![]() 时,
时, ![]() 在
在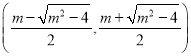 内单调递减,在
内单调递减,在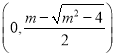 ,
, 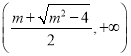 内单调递增.
内单调递增.
(2)由(1)知, ![]() ,所以
,所以![]() 的两根
的两根![]() ,
, ![]() 即为方程
即为方程![]() 的两根.因为
的两根.因为![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() .又因为
.又因为![]() ,
, ![]() 为
为![]() 的零点,
的零点,
所以![]() ,
, ![]() ,两式相减得
,两式相减得![]() ,得
,得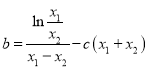 .而
.而![]() ,所以
,所以![]()
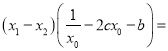

![]()
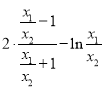 .
.
令![]() ,由
,由![]() 得
得![]() ,因为
,因为![]() ,两边同时除以
,两边同时除以![]() ,得
,得![]() ,因为
,因为![]() ,故
,故![]() ,解得
,解得![]() 或
或![]() ,所以
,所以![]() .设
.设![]() ,所以
,所以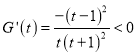 ,则
,则![]() 在
在![]() 上是减函数,所以
上是减函数,所以![]() ,
,
即![]() 的最小值为
的最小值为![]() .
.
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知三角形ABC的顶点坐标为A(﹣1,5)、B(﹣2,﹣1)、C(4,3).
(1)求AB边上的高线所在的直线方程;
(2)求三角形ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景区修建一栋复古建筑,其窗户设计如图所示.圆![]() 的圆心与矩形
的圆心与矩形![]() 对角线的交点重合,且圆与矩形上下两边相切(
对角线的交点重合,且圆与矩形上下两边相切(![]() 为上切点),与左右两边相交(
为上切点),与左右两边相交(![]() ,
, ![]() 为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m,且
为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m,且![]() .设
.设![]() ,透光区域的面积为
,透光区域的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式,并求出定义域;
的函数关系式,并求出定义域;
(2)根据设计要求,透光区域与矩形窗面的面积比值越大越好.当该比值最大时,求边![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信运动和运动手环的普及,增强了人民运动的积极性,每天一万步称为一种健康时尚,某中学在全校范围内内积极倡导和督促师生开展“每天一万步”活动,经过几个月的扎实落地工作后,学校想了解全校师生每天一万步的情况,学校界定一人一天走路不足![]() 千步为不健康生活方式,不少于
千步为不健康生活方式,不少于![]() 千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为
千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为![]() 人,高一学生人数为
人,高一学生人数为![]() 人,高二学生人数
人,高二学生人数![]() 人,高三学生人数
人,高三学生人数![]() ,从中抽取
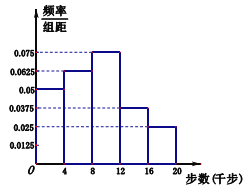
,从中抽取![]() 人作为调查对象,得到了如图所示的这
人作为调查对象,得到了如图所示的这![]() 人的频率分布直方图,这
人的频率分布直方图,这![]() 人中有
人中有![]() 人被学校界定为不健康生活方式者.
人被学校界定为不健康生活方式者.
(1)求这次作为抽样调查对象的教师人数;
(2)根据频率分布直方图估算全校师生每人一天走路步数的中位数(四舍五入精确到整数步);
(3)校办公室欲从全校师生中速记抽取![]() 人作为“每天一万步”活动的慰问对象,计划学校界定不健康生活方式者鞭策性精神鼓励
人作为“每天一万步”活动的慰问对象,计划学校界定不健康生活方式者鞭策性精神鼓励![]() 元,超健康生活方式者表彰奖励
元,超健康生活方式者表彰奖励![]() 元,一般生活方式者鼓励性奖励
元,一般生活方式者鼓励性奖励![]() 元,利用样本估计总体,将频率视为概率,求这次校办公室慰问奖励金额恰好为
元,利用样本估计总体,将频率视为概率,求这次校办公室慰问奖励金额恰好为![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信运动和运动手环的普及,增强了人民运动的积极性,每天一万步称为一种健康时尚,某中学在全校范围内内积极倡导和督促师生开展“每天一万步”活动,经过几个月的扎实落地工作后,学校想了解全校师生每天一万步的情况,学校界定一人一天走路不足![]() 千步为不健康生活方式,不少于
千步为不健康生活方式,不少于![]() 千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为
千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为![]() 人,高一学生人数为
人,高一学生人数为![]() 人,高二学生人数
人,高二学生人数![]() 人,高三学生人数
人,高三学生人数![]() ,从中抽取
,从中抽取![]() 人作为调查对象,得到了如图所示的这
人作为调查对象,得到了如图所示的这![]() 人的频率分布直方图,这
人的频率分布直方图,这![]() 人中有
人中有![]() 人被学校界定为不健康生活方式者.
人被学校界定为不健康生活方式者.
(1)求这次作为抽样调查对象的教师人数;
(2)根据频率分布直方图估算全校师生每人一天走路步数的中位数(四舍五入精确到整数步);
(3)校办公室欲从全校师生中速记抽取![]() 人作为“每天一万步”活动的慰问对象,计划学校界定不健康生活方式者鞭策性精神鼓励
人作为“每天一万步”活动的慰问对象,计划学校界定不健康生活方式者鞭策性精神鼓励![]() 元,超健康生活方式者表彰奖励
元,超健康生活方式者表彰奖励![]() 元,一般生活方式者鼓励性奖励
元,一般生活方式者鼓励性奖励![]() 元,利用样本估计总体,将频率视为概率,求这次校办公室慰问奖励金额恰好为
元,利用样本估计总体,将频率视为概率,求这次校办公室慰问奖励金额恰好为![]() 元的概率.
元的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,其前n项和为Sn , {bn}是等比数列,且a1=b1=2,a4+b4=27,S4﹣b4=10.
(1)求数列{an}与{bn}的通项公式;
(2)记Tn=anb1+an﹣1b2+…+a1bn , n∈N* , 是否存在实数p,q,r,对于任意n∈N* , 都有Tn=pan+qbn+r,若存在求出p,q,r的值,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosxsin(x+ ![]() )﹣
)﹣ ![]() .
.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)△ABC中,角A,B,C所对的边为a,b,c,f( ![]() )=
)= ![]() ,B=
,B= ![]() ,a=1,求△ABC的面积.
,a=1,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68),再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的比例 |
第1组 | [18,28) | 5 | 0.5 |
第2组 | [28,38) | 18 | a |
第3组 | [38,48) | 27 | 0.9 |
第4组 | [48,58) | x | 0.36 |
第5组 | [58,68) | 3 | 0.2 |

(1)分别求出a,x的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为3 ![]() ,b﹣c=2,cosA=﹣
,b﹣c=2,cosA=﹣ ![]() .
.
(1)求a和sinC的值;
(2)求cos(2A+ ![]() )的值.
)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com