
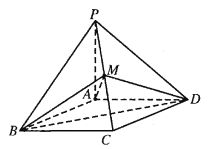
【题目】如图,四棱锥![]() 的底面
的底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() 平面
平面![]() ,点
,点![]() 是棱
是棱![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)当![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点,由三角形中位线定理可得
中点,由三角形中位线定理可得![]() ,从而可得结论;(2)取线段
,从而可得结论;(2)取线段![]() 的中点
的中点![]() ,先证明
,先证明![]() 垂直于平面
垂直于平面![]() ,则点
,则点![]() 到平面
到平面![]() 的距离即为
的距离即为![]() 的长度. 结合
的长度. 结合![]() A
A![]() ,可得点
,可得点![]() 到平面
到平面![]() 的距离即为
的距离即为![]() 的长度. 由
的长度. 由![]() 为
为![]() 的中点,可得点
的中点,可得点![]() 到平面
到平面![]() 的距离即为
的距离即为![]() 的长度,利用
的长度,利用![]() 即可得结果.
即可得结果.
(1)如图,
连接AC交BD于点O,连接MO.
∵M,O分别为PC,AC中点,
∴PA∥MO ,
∵PA不在平面BMD内,MO![]() 平面BMD.
平面BMD.
∴PA∥平面BMD.
(2)如图,取线段BC的中点H,连结AH.
∵ABCD是菱形,![]() ,∴AH⊥AD.
,∴AH⊥AD.
∵PA⊥平面ABCD,∴AH⊥PA.
又PA∩AD=A,PA,AD![]() 平面PAD.
平面PAD.
AH⊥平面PAD.∴点H到平面PAD的距离即为AH的长度.
∴BC∥AD,∴点C到平面PAD的距离即为AH的长度.
∵M为PC的中点,∴点M到平面PAD的距离即为![]() AH的长度.
AH的长度.
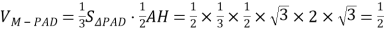
![]() .
.


科目:高中数学 来源: 题型:
【题目】某市每年春节前后,由于大量的烟花炮竹的燃放,空气污染较为严重.该市环保研究所对近年春节前后每天的空气污染情况调查研究后发现,每天空气污染的指数.f(t),随时刻t(时)变化的规律满足表达式![]() ,其中a为空气治理调节参数,且a∈(0,1).
,其中a为空气治理调节参数,且a∈(0,1).
(1)令![]() ,求x的取值范围;
,求x的取值范围;
(2)若规定每天中f(t)的最大值作为当天的空气污染指数,要使该市每天的空气污染指数不超过5,试求调节参数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线
轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() .若直
.若直![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理也就是“等积原理”,它是由我国南北朝杰出的数学家祖冲之的儿子祖暅首先提出来的.祖暅原理的内容是:“幂势既同,则积不容异”,“势”即是高,“幂”是面积.意思是,如果夹在两平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果两个截面的面积总相等,那么这两个几何体的体积相等.已知,两个平行平面间有三个几何体,分别是三棱锥、四棱锥、圆锥(高度都是h),其中:三棱锥的体积为V,四棱锥的底面是边长为a的正方形,圆锥的底面半径为r,现用平行于这两个平面的平面去截三个几何体,如果得到的三个截面面积总相等,那么,下面关系式正确的是( )
A.![]() ,
,![]() ,
,![]() B.
B.![]() ,
,![]() ,
,![]()
C.![]() ,
,![]() ,
,![]() D.
D.![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小型企业甲产品生产的投入成本x(单位:万元)与产品销售收入y(单位:万元)存在较好的线性关系,下表记录了最近5次该产品的相关数据.
x(万元) | 3 | 5 | 7 | 9 | 11 |
y(万元) | 8 | 10 | 13 | 17 | 22 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大(毛利率![]()
![]()
![]() )?
)?
相关公式: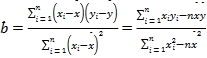 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
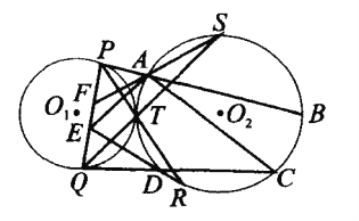
【题目】如图,两圆外切于点T, PQ为![]() 的弦,直线PT、QT分别交
的弦,直线PT、QT分别交![]() 于点R、S,分别过P、Q作
于点R、S,分别过P、Q作![]() 的切线依次交
的切线依次交![]() 于A、B、D、C,直线RD、SA分别交PQ于E、F。求证:
于A、B、D、C,直线RD、SA分别交PQ于E、F。求证:![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,底面是边长为4的正三角形,
中,底面是边长为4的正三角形,![]() ,
,![]() 底面
底面![]() ,点
,点![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com