解:因为根据三角形的正弦定理和余弦定理,我们可以解得,只有c选项中有两个解。D无解,A,B一解。
A、由A和C的度数,利用三角形的内角和定理求出B的度数,由sinA,sinC及sinB,还有b的值,利用正弦定理求出a与c的值,得到此三角形只有一解,本选项错误;
B、由a,c及cosB的值,利用余弦定理求出b的值,得到此三角形只有一解,本选项错误;
C、由a小于c,得到A小于C,由A为钝角,得到C也为钝角,不能构成三角形,故此三角形无解;
D、由a,c及sinA的值,利用正弦定理求出sinC的值,且得到sinC的值大于
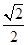
,同时由a小于c得到C小于45°,根据正弦函数的图象与性质得到C的度数有两解,故此三角形有两解,本选项正确.
解:A、由A=45°,C=80°,得到B=55°,
根据正弦定理
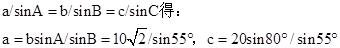
则此时三角形只有一解,本选项错误;
B、由a=30,c=28,B=60°,
根据余弦定理得:b
2=a
2+c
2-2accosB=844,
解得b=
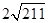
,即此三角形只有一解,
本选项错误;
C、由a=12,c=15,得到a<c,
有A<C,而A=120°,得到C也为钝角,
则此三角形无解,本选项错误;
D、由a=14,c=16,A=45°,
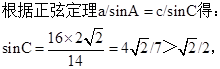
又c>a,得到C>45°,
根据正弦函数的图象与性质得到C有两解,本选项正确,
故选C

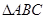 ,其中有两解的是
,其中有两解的是
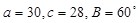
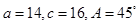
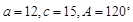
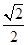 ,同时由a小于c得到C小于45°,根据正弦函数的图象与性质得到C的度数有两解,故此三角形有两解,本选项正确.
,同时由a小于c得到C小于45°,根据正弦函数的图象与性质得到C的度数有两解,故此三角形有两解,本选项正确.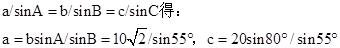
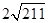 ,即此三角形只有一解,
,即此三角形只有一解,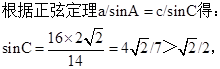


 53随堂测系列答案
53随堂测系列答案