练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设f（x）= ，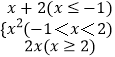
    （1）在下列直角坐标系中画出f（x）的图象；

    （2）若f（x）=3，求x的值；
    （3）看图象写出函数f（x）的值域．

    【答案】
    （1）解：根据f（x）= ，画出它的图象，

    如图：


    （2）解：由f（x）=3，可得x2=3，∴x= （负的舍去）
    （3）解：看图象写出函数f（x）的值域为（﹣∞，+∞）
    【解析】根据函数的解析式，画出它的图象，数形结合可得结论．
    【考点精析】根据题目的已知条件，利用函数的值域的相关知识可以得到问题的答案，需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某厂有4台大型机器，在一个月中，一台机器至多出现1次故障，且每台机器是否出现故障是相互独立的，出现故障时需1名工人进行维修，每台机器出现故障需要维修的概率为.

    (1)若出现故障的机器台数为，求的分布列；

    (2) 该厂至少有多少名工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%？

    (3)已知一名工人每月只有维修1台机器的能力，每月需支付给每位工人1万元的工资，每台机器不出现故障或出现故障能及时维修，就使该厂产生5万元的利润，否则将不产生利润，若该厂现有2名工人，求该厂每月获利的均值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）求函数的最大值；

    （2）设 其中，证明: ＜1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）是定义在R上的减函数，且f（x）＞0恒成立，若对任意的x，y∈R，都有f（x﹣y）= ，
    （1）求f（0）的值，并证明对任意的x，y∈R，f（x+y）=f（x）f（y）；
    （2）若f（﹣1）=3，解不等式 ≤9．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列四组函数中，表示同一函数的是（ ）
    A.f（x）=|x|，g（x）=
    B.f（x）=lg x2 ， g（x）=2lg x
    C.f（x）= ，g（x）=x+1
    D.f（x）= ? ，g（x）=

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中为自然对数的底数．（参考数据： ）

    （1）讨论函数的单调性；

    （2）若时，函数有三个零点，分别记为，证明： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设定义在R上的偶函数f（x）满足f（x+2）=f（x），f′（x）是f（x）的导函数，当x∈[0，1]时，0≤f（x）≤1；当x∈（0，2）且x≠1时，x（x﹣1）f′（x）＜0．则方程f（x）=lg|x|根的个数为（ ）
    A.12
    B.1 6
    C.18
    D.20

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法中，正确的是 ． （填序号）
    ①若集合A={x|kx2+4x+4=0}中只有一个元素，则k=1；
    ②在同一平面直角坐标系中，y=2x与y=2﹣x的图象关于y轴对称；
    ③y=（ ）﹣x是增函数；
    ④定义在R上的奇函数f（x）有f（x）f（﹣x）≤0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】等差数列{an}的前n项和为Sn ， 已知a1=10，a2为整数，且Sn≤S4 ， 设 ，则数列{bn}的前项和Tn为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案