Question

某地区为响应上级号召，在2011年初，新建了一批有200万平方米的廉价住房，供困难的城市居民居住．由于下半年受物价的影响，根据本地区的实际情况，估计今后住房的年平均增长率只能达到5%.

(1)经过x年后，该地区的廉价住房为y万平方米，求y＝f(x)的表达式，并求此函数的定义域．

(2)作出函数y＝f(x)的图象，并结合图象求：经过多少年后，该地区的廉价住房能达到300万平方米？

 

Answer 1

【答案】

(1) y＝200(1＋5%)^x(x∈N^*)

(2) 经过9年后，该地区的廉价住房能达到300万平方米

【解析】解：(1)经过1年后，廉价住房面积为

200＋200×5%＝200(1＋5%)；

经过2年后为200(1＋5%)²；

　…

经过x年后，廉价住房面积为200(1＋5%)^x，

∴y＝200(1＋5%)^x(x∈N^*)．

(2)作函数y＝f(x)＝200(1＋5%)^x(x≥0)的图象，如图所示．

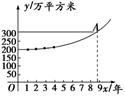
作直线y＝300，与函数y＝200(1＋5%)^x的图象交于A点，则A(x_0,300)，A点的横坐标x₀的值就是函数值y＝300时所经过的时间x的值．

因为8<x₀<9，则取x₀＝9，

即经过9年后，该地区的廉价住房能达到300万平方米．