
【题目】学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同.每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在1次游戏中,
①摸出3个白球的概率;
②获奖的概率;
(2)求在2次游戏中获奖次数![]() 的分布列.
的分布列.
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的半焦距为
的半焦距为![]() ,圆
,圆![]() 与椭圆
与椭圆![]() 有且仅有两个公共点,直线
有且仅有两个公共点,直线![]() 与椭圆
与椭圆![]() 只有一个公共点.
只有一个公共点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知动直线![]() 过椭圆
过椭圆![]() 的左焦点
的左焦点![]() ,且与椭圆
,且与椭圆![]() 分别交于
分别交于![]() 两点,试问:
两点,试问:![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出该定值和点
为定值?若存在,求出该定值和点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,![]() ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.

(1)求证:AC ⊥BC1;
(2)求证:AC 1 // 平面CDB1;
(3)(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ex+asinx,x∈(-π,+∞),下列说法正确的是( )
A.当a=1时,f(x)在(0,f(0))处的切线方程为2x-y+1=0
B.当a=1时,f(x)存在唯一极小值点x0且-1<f(x0)<0
C.对任意a>0,f(x)在(-π,+∞)上均存在零点
D.存在a<0,f(x)在(-π,+∞)上有且只有一个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直三棱柱![]() 中的底面为等腰直角三角形,
中的底面为等腰直角三角形,![]() ,点
,点![]() 分别是边
分别是边![]() ,
,![]() 上动点,若直线
上动点,若直线![]() 平面
平面![]() ,点
,点![]() 为线段
为线段![]() 的中点,则
的中点,则![]() 点的轨迹为
点的轨迹为![]()
![]()
A. 双曲线的一支![]() 一部分
一部分![]() B. 圆弧
B. 圆弧![]() 一部分
一部分![]()
C. 线段![]() 去掉一个端点
去掉一个端点![]() D. 抛物线的一部分
D. 抛物线的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,公园里有一湖泊,其边界由两条线段![]() 和以
和以![]() 为直径的半圆弧
为直径的半圆弧![]() 组成,其中
组成,其中![]() 为2百米,
为2百米,![]() 为
为![]() .若在半圆弧
.若在半圆弧![]() ,线段
,线段![]() ,线段
,线段![]() 上各建一个观赏亭
上各建一个观赏亭![]() ,再修两条栈道
,再修两条栈道![]() ,使
,使![]() . 记
. 记![]() .
.
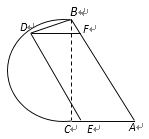
(1)试用![]() 表示
表示![]() 的长;
的长;
(2)试确定点![]() 的位置,使两条栈道长度之和最大.
的位置,使两条栈道长度之和最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在A,B实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图.记综合评分为80及以上的花苗为优质花苗.
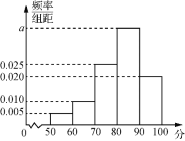
(1)求图中a的值;
(2)用样本估计总体,以频率作为概率,若在A,B两块试验地随机抽取3棵花苗,求所抽取的花苗中的优质花苗数的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com