
【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择.
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率均为![]() ,第一次抽奖,若未中奖,则抽奖结束,若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖。规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,则获得1000元;若未中奖,则所获得奖金为0元.
,第一次抽奖,若未中奖,则抽奖结束,若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖。规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,则获得1000元;若未中奖,则所获得奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为![]() ,每次中奖均可获得奖金400元.
,每次中奖均可获得奖金400元.
(1)求某员工选择方案甲进行抽奖所奖金![]() (元)的分布列;
(元)的分布列;
(2)试比较某员工选择方案乙与选择方案甲进行抽奖,哪个方案更划算?
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,|φ|< ![]() )其中的图象如图所示,为了得到g(x)=cos(2x﹣
)其中的图象如图所示,为了得到g(x)=cos(2x﹣ ![]() )的图象,只需将f(x)的图象( )
)的图象,只需将f(x)的图象( ) 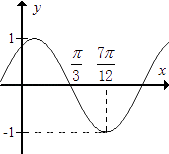
A.向左平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区拟建立一个艺术博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从![]() 个招标问题中随机抽取
个招标问题中随机抽取![]() 个问题,已知这
个问题,已知这![]() 个招标问题中,甲公司可正确回答其中的
个招标问题中,甲公司可正确回答其中的![]() 道題目,而乙公司能正确回答毎道题目的概率均为
道題目,而乙公司能正确回答毎道题目的概率均为![]() ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
(1)求甲、乙两家公司共答对![]() 道题目的概率;
道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2ωx﹣sin2ωx+2 ![]() cosωxsinωx,其中ω>0,若f(x)相邻两条对称轴间的距离不小于
cosωxsinωx,其中ω>0,若f(x)相邻两条对称轴间的距离不小于 ![]()
(1)求ω的取值范围及函数f(x)的单调递增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,a= ![]() ,b+c=3,当ω最大时,f(A)=1,求sinBsinC的值.
,b+c=3,当ω最大时,f(A)=1,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥P﹣ABCD,B1为PB的中点,D1为PD的中点,则两个棱锥A﹣B1CD1 , P﹣ABCD的体积之比是( ) 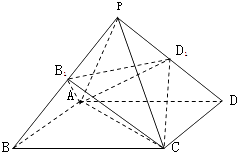
A.1:4
B.3:8
C.1:2
D.2:3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1=1,a2=2,且an+1=2an+3an﹣1(n≥2,n∈N+).
(1)设bn=an+1+an(n∈N+),求证{bn}是等比数列;
(2)(i)求数列{an}的通项公式;
(ii)求证:对于任意n∈N+都有 ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() <
< ![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正项数列{an}前n项和为Sn , 且 ![]() (n∈N+)
(n∈N+)
(1)求数列{an}的通项公式;
(2)若 ![]() ,数列{bn}的前n项和为Tn , 证明:T2n﹣1>1>T2n(n∈N+).
,数列{bn}的前n项和为Tn , 证明:T2n﹣1>1>T2n(n∈N+).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com