
【题目】若二次函数f(x)=ax2+bx+c(a、b∈R)满足f(x+1)﹣f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)若在区间[﹣1,﹣1]上,不等式f(x)>2x+m恒成立,求实数m的取值范围.
【答案】
(1)解:由f(0)=1得,c=1.∴f(x)=ax2+bx+1
又f(x+1)﹣f(x)=2x,∴a(x+1)2+b(x+1)+1﹣(ax2+bx+1)=2x,
即2ax+a+b=2x,
∴ ![]() ,解得
,解得 ![]()
∴f(x)=x2﹣x+1
(2)解:f(x)>2x+m等价于x2﹣x+1>2x+m,即x2﹣3x+1﹣m>0,
要使此不等式在[﹣1,﹣1]上恒成立,只需使函数g(x)=x2﹣3x+1﹣m在[﹣1,﹣1]的最小值大于0即可.
∵g(x)=x2﹣3x+1﹣m在[﹣1,﹣1]上单调递减,
∴g(x)min=g(1)=﹣m﹣1,
由﹣m﹣1>0,得m<﹣1
∴实数m的取值范围是(﹣∞,﹣1)
【解析】(1)由f(0)=1,求出c=1,根据f(x+1)﹣f(x)=2x,通过系数相等,从而求出a,b的值;(2)f(x)>2x+m等价于x2﹣x+1>2x+m,即x2﹣3x+1﹣m>0,要使此不等式在[﹣1,﹣1]上恒成立,只需使函数g(x)=x2﹣3x+1﹣m在[﹣1,﹣1]的最小值大于0即可,求出g(x)的最小值即可.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)+kx与g(x)=log4(a2x﹣ ![]() a),其中f(x)是偶函数.
a),其中f(x)是偶函数.
(1)求实数k的值;
(2)求函数g(x)的定义域;
(3)若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于两条平行直线和圆的位置关系定义如下:若两直线中至少有一条与圆相切,则称该位置关系为“平行相切”;若两直线都与圆相离,则称该位置关系为“平行相离”;否则称为“平行相交”.已知直线l1:ax+3y+6=0,l2:2x+(a+1)y+6=0与圆C:x2+y2+2x=b2-1(b>0)的位置关系是“平行相交”,则实数b的取值范围为 ( )
A. (![]() ,
, ![]() ) B. (0,
) B. (0, ![]() )
)
C. (0, ![]() ) D. (
) D. (![]() ,
, ![]() )∪(
)∪(![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示的平面图形中,ABCD是边长为2的正方形,△HDA和△GDC都是以D为直角顶点的等腰直角三角形,点E是线段GC的中点.现将△HDA和△GDC分别沿着DA,DC翻折,直到点H和G重合为点P.连接PB,得如图2的四棱锥. 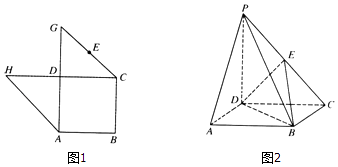
(Ⅰ)求证:PA∥平面EBD;
(Ⅱ)求二面角C﹣PB﹣D大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】知f(x)是定义在R上的奇函数,且当x∈(0,+∞)时,f(x)=2018x+log2018x,则函数f(x)的零点个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=xlnx,g(x)=﹣x2+ax﹣3.
(1)求函数f(x)在[t,t+2](t>0)上的最小值;
(2)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:(k-3)x+(4-k)y+1=0与l2:2(k-3)x-2y+3=0.
(1)若这两条直线垂直,求k的值;
(2)若这两条直线平行,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个多面体的直观图、正视图、侧视图、俯视图如图,M,N分别为A1B,B1C1的中点.
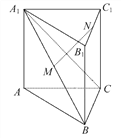
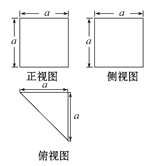
下列结论中正确的个数有 ( )
①直线MN与A1C相交.
②MN⊥BC.
③MN∥平面ACC1A1.
④三棱锥N-A1BC的体积为![]() =
=![]() a3.
a3.
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数y=f(x)满足f(3)=0,且当x>0时,不等式f(x)>﹣xf′(x)恒成立,则函数g(x)=xf(x)的零点的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com