甲、乙、丙三个盒子,甲盒中有5个白球,乙盒中有4个白球1个黑球,丙盒中有3个白球2个黑球,从每个盒中取2个球(取到每球的可能性相等).
求:(1)只取到一个黑球的概率;
(2)取到两个黑球的概率.
【答案】
分析:(1)本题是一个相互独立事件同时发生的概率,只取到一个黑球,有两种情况,一是从乙盒中取一个黑球和一个白球,从丙盒中取两个白球;一是从乙盒中取两个白球,从丙盒中取一个白球和一个黑球,这两种情况是互斥的.
(2)本题是一个相互独立事件同时发生的概率,只取到两个黑球,有两种情况,一是从乙盒中取一黑一白,从丙盒中取一黑一白,一是从乙盒中取两个白球,从丙盒中取两个黑球,这两种情况是互斥的.
解答:解:(1)由题意知本题是一个相互独立事件同时发生的概率,
从每一个盒中取两个球,只取到一个黑球,有两种情况,
一是从乙盒中取一个黑球和一个白球,从丙盒中取两个白球;
一是从乙盒中取两个白球,从丙盒中取一个白球和一个黑球,这两种情况是互斥的,
∴只取到一个白球的概率是

=

(2)由题意知本题是一个相互独立事件同时发生的概率,
从每一个盒中取两个球,只取到两个黑球,有两种情况,
一是从乙盒中取一黑一白,从丙盒中取一黑一白,
一是从乙盒中取两个白球,从丙盒中取两个黑球,这两种情况是互斥的
∴取到两个黑球的概率是

=

即只取到一个白球的概率是
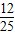
,取到两个黑球的概率是
 点评:
点评:本题考查 互斥事件的概率和相互独立事件同时发生的概率,本题解题的关键是看出所包含的事件由几种情况,每一种情况的基本事件数是多少,本题是一个基础题.

 =
=
 =
=
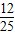 ,取到两个黑球的概率是
,取到两个黑球的概率是


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案