
科目:高中数学 来源: 题型:
|
| A、24.0元 |
| B、40.8元 |
| C、48.0元 |
| D、64.8元 |
查看答案和解析>>
科目:高中数学 来源: 题型:044
物理学家James.D.Forbes试图通过水的沸点来估计海拔高度,他知道通过气压计测得的大气压可用于得到海拔高度,气压越低,高度越高,他测量了17个地方水的沸点(℉)及大气压数据,并且对数据作了简单的处理,得到了较为明确的数学关系,所提数据如下:
|
测点编号 |
沸点(℉) |
气压 |
1g(气压) |
100´1g(气压) |
|
1 |
194.5 |
20.79 |
1.3179 |
131.79 |
|
2 |
194.3 |
20.79 |
1.3179 |
131.79 |
|
3 |
197.9 |
22.40 |
1.3502 |
135.02 |
|
4 |
198.4 |
22.67 |
1.3555 |
135.55 |
|
5 |
199.4 |
23.15 |
1.3646 |
136.46 |
|
6 |
199.9 |
23.35 |
1.3683 |
136.83 |
|
7 |
200.9 |
23.89 |
1.3782 |
137.82 |
|
8 |
201.1 |
23.99 |
1.3800 |
138.00 |
|
9 |
201.4 |
24.02 |
1.3805 |
138.05 |
|
10 |
201.3 |
24.01 |
1.3806 |
138.06 |
|
11 |
203.6 |
25.14 |
1.4004 |
140.04 |
|
12 |
204.6 |
26.57 |
1.4244 |
142.44 |
|
13 |
209.5 |
28.49 |
1.4547 |
145.47 |
|
15 |
208.6 |
27.76 |
1.4434 |
144.34 |
|
15 |
210.7 |
29.04 |
1.4630 |
146.30 |
|
16 |
211.9 |
29.88 |
1.4754 |
147.54 |
|
17 |
212.2 |
30.06 |
1.4780 |
147.80 |
(1)试作出气压y=100´1g(气压)关于沸点(℉)的散点图;
(2)根据散点图判断变量x与y的相关关系;计算变量x与y的相关系数;
(3)建立变量x与y的一元线性回归方程。
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
|
测点编号 |
沸点(℉) |
气压 |
1g(气压) |
100´1g(气压) |
|
1 |
194.5 |
20.79 |
1.3179 |
131.79 |
|
2 |
194.3 |
20.79 |
1.3179 |
131.79 |
|
3 |
197.9 |
22.40 |
1.3502 |
135.02 |
|
4 |
198.4 |
22.67 |
1.3555 |
135.55 |
|
5 |
199.4 |
23.15 |
1.3646 |
136.46 |
|
6 |
199.9 |
23.35 |
1.3683 |
136.83 |
|
7 |
200.9 |
23.89 |
1.3782 |
137.82 |
|
8 |
201.1 |
23.99 |
1.3800 |
138.00 |
|
9 |
201.4 |
24.02 |
1.3805 |
138.05 |
|
10 |
201.3 |
24.01 |
1.3806 |
138.06 |
|
11 |
203.6 |
25.14 |
1.4004 |
140.04 |
|
12 |
204.6 |
26.57 |
1.4244 |
142.44 |
|
13 |
209.5 |
28.49 |
1.4547 |
145.47 |
|
15 |
208.6 |
27.76 |
1.4434 |
144.34 |
|
15 |
210.7 |
29.04 |
1.4630 |
146.30 |
|
16 |
211.9 |
29.88 |
1.4754 |
147.54 |
|
17 |
212.2 |
30.06 |
1.4780 |
147.80 |
(1)试作出气压y=100´1g(气压)关于沸点(℉)的散点图;
(2)根据散点图判断变量x与y的相关关系;计算变量x与y的相关系数;
(3)建立变量x与y的一元线性回归方程。
查看答案和解析>>
科目:高中数学 来源:2009-2010学年北京市东城区高三会考考前练习数学试卷(解析版) 题型:选择题
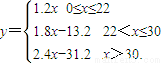 如果甲、乙两户某月用水量分别为20立方米、40立方米,那么该月乙户应比甲户多交水费( )
如果甲、乙两户某月用水量分别为20立方米、40立方米,那么该月乙户应比甲户多交水费( )查看答案和解析>>
科目:高中数学 来源:2014届河南省郑州市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
某同学为了解秋冬季节用电量(y度)与气温(x℃)的关系曾由下表数据计算出回归直线方程为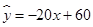 ,现表中有一个数据被污损。则被污损的数据为
,现表中有一个数据被污损。则被污损的数据为
|
气温 |
18 |
13 |
10 |
—1 |
|
用电量(度) |
24 |
34 |
* |
64 |
A.40 B.39 C.38 D.37
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com