
����Ŀ��ij��λ�⽨һ���Ȼ���״�Ļ�̳����ͼ��ʾ���������Ҫ���Ȼ����ܳ�Ϊ30�ף����д�Բ������Բ�İ뾶Ϊ10�ף���СԲ������Բ�İ뾶Ϊx�ף�Բ�Ľ�Ϊ�ȣ����ȣ��� 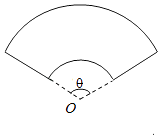
��1����ȹ���x�ĺ�����ϵʽ��
��2����֪�Ի�̳�ı�Ե��ʵ�߲��֣�����װ��ʱ��ֱ�߲��ֵ�װ�η���Ϊ4Ԫ/�ף����߲��ֵ�װ�η���Ϊ9Ԫ/�ף��軨̳�������װ���ܷ���֮��Ϊy����y����x�ĺ�����ϵʽ�������y�����ֵ��
���𰸡�
��1���⣺�����֪30=�ȣ�10+x��+2��10��x�������Ԧ�= ![]() ��x�ʣ�0��10��
��x�ʣ�0��10��
��2���⣺��̳�����Ϊ ![]() �ȣ�102��x2��=��5+x����10��x��=��x2+5x+50��0��x��10����
�ȣ�102��x2��=��5+x����10��x��=��x2+5x+50��0��x��10����
װ���ܷ���Ϊ9�ȣ�10+x��+8��10��x��=170+10x��
���Ի�̳�������װ���ܷ���֮��Ϊy= ![]() =��
=�� ![]() ��
��
��t=17+x��t�ʣ�17��27����y= ![]() ��
�� ![]() ��t+
��t+ ![]() ����
���� ![]() ��
�� ![]() =
= ![]() ��
��
���ҽ���t=18ʱȡ�Ⱥţ���ʱx=1����= ![]() ��
��
��������˫����������������ֵ�ģ���ͬ�ȱ����֣�����˵�������ԣ���
�ʵ�x=1ʱ����̳�������װ���ܷ���֮�����
����������1���������ε��ܳ���ʽ������⼴�ɣ���2����ϻ�̳�������ʽ����Ϸ���֮��Ĺ�ϵ������⼴�ɣ�


 ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC���ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c����֪2cosC��acosB+bcosA��=c��
��1�����C��
��2���� ![]() ����ABC�����Ϊ
����ABC�����Ϊ ![]() ����a+b��ֵ��
����a+b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��
�� ![]() ������
������ ![]() ��
�� ![]() ��k��R��
��k��R��
��1����kΪ��ֵʱ���� ![]() ��
�� ![]() ��
��
��2�������� ![]() ��
�� ![]() �ļн�Ϊ�۽ǣ���ʵ��k��ȡֵ��Χ��
�ļн�Ϊ�۽ǣ���ʵ��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȳ�����{an}��ǰn���ΪSn= ![]() ��3n+5��������ȱ�����{bn}�У�b2=4��b1b7=256��
��3n+5��������ȱ�����{bn}�У�b2=4��b1b7=256��
��1����{an}��{bn}��ͨ�ʽ��
��2����cn=anbn �� ��{cn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC���ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c����btanB= ![]() ��
��
��1�����B��ֵ��
��2������ABC�����Ϊ ![]() ��a+c=8�����b��
��a+c=8�����b��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ����A��B���ֲ�Ʒ������ÿһ�ֲ�Ʒ������Ͷ�����ú�͵�������
��ƷƷ�� | �Ͷ��������� | ú���֣� | �磨ǧ�ߣ� |
A��Ʒ | 3 | 9 | 4 |
B��Ʒ | 10 | 4 | 5 |
��֪����ÿ��A��Ʒ��������7��Ԫ������ÿ��B��Ʒ��������12��Ԫ�������������ƣ�����ҵ�����Ͷ���300����ú360�֣����ҹ����ֻ�ܹ���200ǧ�ߣ����ʸ���ҵ��ΰ������������ܻ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=sinxcos2x�����н�����ȷ���ǣ� ��
A.y=f��x����ͼ����� ![]() �Գ�
�Գ�
B.y=f��x����ͼ����� ![]() �Գ�
�Գ�
C.y=f��x����ͼ�����y��Գ�
D.y=f��x���������ں���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Χ��һ�����Ϊ360m2�ľ��γ��أ�Ҫ����γ��ص�һ�����þ�ǽ�����þ�ǽ��ά�ޣ�����������ΧǽҪ�½����ھ�ǽ�Ķ������ǽ��Ҫ��һ������Ϊ2m�Ľ����ڣ���֪��ǽ��ά����Ϊ45Ԫ/m����ǽ�����Ϊ180Ԫ/m�������õľ�ǽ�ij���Ϊx����λ��m�������˾��γ���Χǽ���ܷ���Ϊy����λ��Ԫ���� ����y��ʾΪx�ĺ�����
������ȷ��x��ʹ���˾��γ���Χǽ���ܷ�����С���������С�ܷ��ã�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com