
【题目】已知函数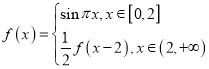 ,有下列说法:
,有下列说法:
①函数![]() 对任意
对任意![]() ,都有
,都有![]() 成立;
成立;
②函数![]() 在
在![]() 上单调递减;
上单调递减;
③函数![]() 在
在![]() 上有3个零点;
上有3个零点;
④若函数![]() 的值域为
的值域为![]() ,设
,设![]() 是
是![]() 中所有有理数的集合,若简分数
中所有有理数的集合,若简分数![]() (其中
(其中![]() ,
,![]() 为互质的整数),定义函数
为互质的整数),定义函数![]() ,则
,则![]() 在
在![]() 中根的个数为5;
中根的个数为5;
其中正确的序号是______(填写所有正确结论的番号).
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 是某景区的两条道路(宽度忽略不计,
是某景区的两条道路(宽度忽略不计,![]() 为东西方向),Q为景区内一景点,A为道路
为东西方向),Q为景区内一景点,A为道路![]() 上一游客休息区,已知
上一游客休息区,已知![]() ,
,![]() (百米),Q到直线
(百米),Q到直线![]() ,
,![]() 的距离分别为3(百米),
的距离分别为3(百米),![]() (百米),现新修一条自A经过Q的有轨观光直路并延伸至道路
(百米),现新修一条自A经过Q的有轨观光直路并延伸至道路![]() 于点B,并在B处修建一游客休息区.
于点B,并在B处修建一游客休息区.
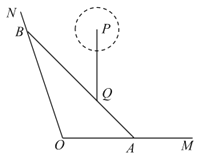
(1)求有轨观光直路![]() 的长;
的长;
(2)已知在景点Q的正北方6百米的P处有一大型组合音乐喷泉,喷泉表演一次的时长为9分钟,表演时,喷泉喷洒区域以P为圆心,r为半径变化,且t分钟时,![]() (百米)(
(百米)(![]() ,
,![]() ).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道
).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道![]() 以
以![]() (百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
(百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)若曲线![]() 与曲线
与曲线![]() 在它们的交点
在它们的交点![]() 处具有公共切线,求a,b的值;
处具有公共切线,求a,b的值;
(2)当![]() 时,若函数
时,若函数![]() 在区间
在区间![]() 内恰有两个零点,求a的取值范围;
内恰有两个零点,求a的取值范围;
(3)![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了改善居民的休闲娱乐活动场所,现有一块矩形![]() 草坪如下图所示,已知:
草坪如下图所示,已知:![]() 米,
米,![]() 米,拟在这块草坪内铺设三条小路
米,拟在这块草坪内铺设三条小路![]() 、
、![]() 和
和![]() ,要求点
,要求点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 时上,且
时上,且![]() .
.

(1)设![]() ,试求
,试求![]() 的周长
的周长![]() 关于
关于![]() 的函数解析式,并求出此函数的定义域;
的函数解析式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为![]() 元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com