设f(x)是定义在[0,1]上的函数,若存在x*∈(0,1),使得f(x)在[0,x•]上单调递增,在[x•,1]单调递减,则称f(x)为[0,1]上的单峰函数,x•为峰点,包含峰点的区间为含峰区间.
对任意的[0,1]上的单峰函数f(x),下面研究缩短其含峰区间长度的方法.
(Ⅰ)证明:对任意的x1,x2∈(0,1),x1<x2,若f(x1)≥f(x2),则(0,x2)为含峰区间;若f(x1)≤f(x2),则(x1,1)为含峰区间;
(Ⅱ)对给定的r(0<r<0.5),证明:存在x1,x2∈(0,1),满足x2-x1≥2r,使得由(Ⅰ)确定的含峰区间的长度不大于0.5+r;
(Ⅲ)选取x1,x2∈(0,1),x1<x2由(Ⅰ)可确定含峰区间为(0,x2)或(x1,1),在所得的含峰区间内选取x3,由x3与x1或x3与x2类似地可确定是一个新的含峰区间.在第一次确定的含峰区间为(0,x2)的情况下,试确定x1,x2,x3的值,满足两两之差的绝对值不小于0.02且使得新的含峰区间的长度缩短到0.34.
(区间长度等于区间的右端点与左端点之差).
【答案】
分析:(1)本题是一道新定义题,咋一看挺繁琐且无从下手,其实这类新定义题目只需牢牢的抓住题干定义,需要分f(x
1)≥f(x
2)和 f(x
1)≤f(x
2)两类情况讨论分析;
(2)有了(1)的讨论处理,第(2)显的容易一些,只要借助(1)用r把x
1,x
2分别表达出来;
(3)本问题是在第(2)问的基础上又提出的问题,关键是找出以下两组关系式:x
1+x
2=l和x
3+x
1=x
2,
解答:证明:(I)设x*为f(x)的峰点,则由单峰函数定义可知,f(x)在[0,x*]上单调递增,在[x*,1]上单调递减.
当f(x
1)≥f(x
2)时,假设x*∉(0,x
2),则x
1<x
2<x*,从而f(x*)≥f(x
2)>f(x
1),
这与f(x
1)≥f(x
2)矛盾,所以x*∈(0,x
2),即(0,x
2)是含峰区间.
当f(x
1)≤f(x
2)时,假设x*∉(x
1,1),则x*≤x
1<x
2,从而f(x*)≥f(x
1)>f(x
2),
这与f(x
1)≤f(x
2)矛盾,所以x*∈(x
1,1),即(x
1,1)是含峰区间.
(II)由(I)的结论可知:
当f(x
1)≥f(x
2)时,含峰区间的长度为l
1=x
2;
当f(x
1)≤f(x
2)时,含峰区间的长度为l
2=1-x
1;
对于上述两种情况,由题意得
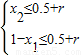
①
由①得1+x
2-x
1≤1+2r,即x
2-x
1≤2r
又因为x
2-x
1≥2r,所以x
2-x
1=2r,②
将②代入①得
x
1≤0.5-r,x
2≥0.5-r,③
由①和③解得x
1=0.5-r,x
2=0.5+r.
所以这时含峰区间的长度l
1=l
1=0.5+r,即存在x
1,x
2使得所确定的含峰区间的长度不大于0.5+r.
(III)解:对先选择的x
1;x
2,x
1<x
2,由(II)可知
x
1+x
2=l,④
在第一次确定的含峰区间为(0,x
2)的情况下,x
3的取值应满足
x
3+x
1=x
2,⑤
由④与⑤可得
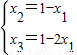
,
当x
1>x
3时,含峰区间的长度为x
1.
由条件x
1-x
3≥0.02,得x
1-(1-2x
1)≥0.02,从而x
1≥0.34.
因此,为了将含峰区间的长度缩短到0.34,只要取x
1=0.34,x
2=0.66,x
3=0.32.
点评:新定义题目一定要注意舍得花时间读懂、理解好定义,这是解决问题的关键所在.另外,证明要注意本题的矛盾手法的使用.本题的是借用新定义的手法考查学生对分段函数的理解和掌握,分段函数的学习一向是高中学习的难点.

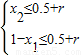 ①
①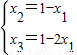 ,
,
