
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{36}$,0) | B. | (0,$\frac{1}{36}$) | C. | ($\frac{9}{4}$,0) | D. | (0,$\frac{9}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
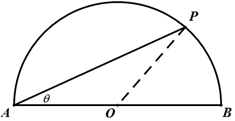 运动员小王在一个如图所示的半圆形水域(O为圆心,AB是半圆的直径)进行体育训练,小王先从点A出发,沿着线段AP游泳至半圆上某点P处,再从点P沿着弧PB跑步至点B处,最后沿着线段BA骑自行车回到点A处,本次训练结束.已知OA=1500m,小王游泳、跑步、骑自行车的平均速度分别为2m/s,4m/s,10m/s,设∠PAO=θrad.
运动员小王在一个如图所示的半圆形水域(O为圆心,AB是半圆的直径)进行体育训练,小王先从点A出发,沿着线段AP游泳至半圆上某点P处,再从点P沿着弧PB跑步至点B处,最后沿着线段BA骑自行车回到点A处,本次训练结束.已知OA=1500m,小王游泳、跑步、骑自行车的平均速度分别为2m/s,4m/s,10m/s,设∠PAO=θrad.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | ±$\frac{2\sqrt{5}}{5}$ | C. | -$\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{265}}}{2}$ | B. | $\frac{{\sqrt{285}}}{2}$ | C. | $\frac{{\sqrt{305}}}{2}$ | D. | $\frac{{\sqrt{335}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com