Question

3．定义在R上的函数f（x）既是偶函数又是周期函数，若f（x）的最小正周期是π，且当x∈[0，$\frac{π}{2}$]时，f（x）=sinx
（1）求当x∈[-$\frac{π}{2}$，0]时，f（x）的解析式；
（2）画出函数f（x）在[-π，π]上的函数简图；
（3）求当f（x）≥$\frac{1}{2}$时，x的取值范围．

Answer 1

分析 （1）首先取x∈[-$\frac{π}{2}$，0]得到-x∈[0，$\frac{π}{2}$]，把-x代入时的解析式，结合偶函数的概念可求得；
（2）作出函数在[-π，0]上的图象，根据偶函数图象关于y轴轴对称得到函数在[0，π]上的图象；
（3）先求出[-π，0]上满足f（x）≥$\frac{1}{2}$时的x的取值范围，根据函数是以π为周期的周期函数，把得到的区间端点值加上π的整数倍得到要求解的区间．

解答 （1）因为f（x）是偶函数，所以f（-x）=f（x）
而当x∈[0，$\frac{π}{2}$]时，f（x）=sinx，
所以x∈[-$\frac{π}{2}$，0]时，-x∈[0，$\frac{π}{2}$]，
f（x）=f（-x）=sin（-x）=-sinx．
所以当x∈[-$\frac{π}{2}$，0]时，f（x）=-sinx，
（2）函数图象如图，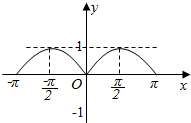

（3）由于f（x）的最小正周期为π，
因此先在[-π，0]上来研究f（x）≥$\frac{1}{2}$时，即-sinx≥$\frac{1}{2}$．
所以sinx≤$-\frac{1}{2}$．所以-$\frac{5π}{6}$≤x≤-$\frac{π}{6}$，．
由周期性知，当f（x）≥$\frac{1}{2}$时，x∈[-$\frac{5π}{6}$+kπ，-$\frac{π}{6}$+kπ]（k∈Z）．
所以，当f（x）≥$\frac{1}{2}$时，x的取值范围是[-$\frac{5π}{6}$+kπ，-$\frac{π}{6}$+kπ]（k∈Z）．

点评 本题考查了函数解析式的求解及常用方法，考查了三角函数的周期及图象，考查了三角函数的奇偶性，解答此题的关键是，通过周期变换和平移变换、把要求解解析式的范围内的变量转化到已知解析式的范围内，此题是中档题．