练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆的离心率，，，是椭圆上三个不同的点，F为其右焦点，且，，成等差数列

    （1）求椭圆的方程；

    （2）求的值；

    （3）若线段AC的垂直平分线与x轴交点为D，求直线BD的斜率k.

    【答案】（1）（2）（3）

    【解析】

    （1）利用椭圆离心率，结合以及点坐标，求得的值，进而求得椭圆的方程.

    （2）利用椭圆的第二定义表示出，根据“” 成等差数列列方程，化简后求得.

    （3）利用点差法求得线段的斜率，由此求得线段的垂直平分线的方程，从而求得点坐标，由此求得直线的斜率.

    （1）∵

    设椭圆方程将点代入得，解得，，，.∴椭圆方程为

    （2）由椭圆第二定义

    同理，

    由于，，成等差数列，所以，化简得

    （3）∵，

    两式相减得

    ∴

    ∴AC的中垂线为

    令得

    ∴.而，

    ∴.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥中，，，为的中点．

    （1）证明：平面；

    （2）若点在棱上，且，求点到平面的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着医院对看病挂号的改革，网上预约成为了当前最热门的就诊方式，这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题；某医院研究人员对其所在地区年龄在10～60岁间的位市民对网上预约挂号的了解情况作出调查，并将被调查的人员的年龄情况绘制成频率分布直方图，如下图所示．

    （Ⅰ）若被调查的人员年龄在20～30岁间的市民有300人，求被调查人员的年龄在40岁以上（含40岁）的市民人数；

    （Ⅱ）若按分层抽样的方法从年龄在以内及以内的市民中随机抽取5人，再从这5人中随机抽取2人进行调研，求抽取的2人中，至多1人年龄在内的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国古代典籍《周易》用“卦”描述万物的变化，每一卦由六爻组成.其中有一种起卦方法称为“金钱起卦法”，其做法为：取三枚相同的钱币合于双手中，上下摇动数下使钱币翻滚摩擦，再随意抛撒钱币到桌面或平盘等硬物上，如此重复六次，得到六爻.若三枚钱币全部正面向上或全部反面向上，就称为变爻.若每一枚钱币正面向上的概率为，则一卦中恰有两个变爻的概率为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，曲线C1的参数方程为（为参数），以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C2：ρ2﹣4ρcosθ+3＝0．

    （1）求曲线C1的一般方程和曲线C2的直角坐标方程；

    （2）若点P在曲线C1上，点Q曲线C2上，求|PQ|的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

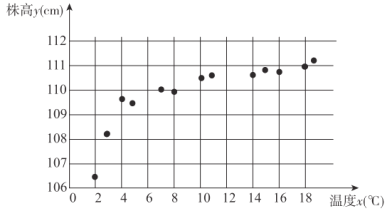
    【题目】一种室内种植的珍贵草药的株高(单位:)与一定范围内的温度(单位:)有关，现收集了该种草药的13组观测数据，得到如下的散点图，现根据散点图利用或建立关于的回归方程,令,,得到如下数据,且与()的相关系数分别为,且.

    10.15

    109.94

    3.04

    0.16

    （1）用相关系数说明哪种模型建立与的回归方程更合适;

    （2）根据（1）的结果及表中数据,建立关于的回归方程;

    （3）已知这种草药的利润与,的关系为，当为何值时，利润的预报值最大.

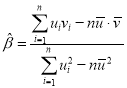    附:参考公式和数据:对于一组数据（）,其回归直线的斜率和截距的最小二乘估计分别为,,相关系数 ,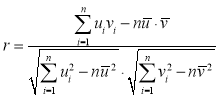

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“共享单车”的出现，为我们提供了一种新型的交通方式。某机构为了调查人们对此种交通方式的满意度，从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20个用户，得到了一个用户满意度评分的样本，并绘制出茎叶图如图：

    （1）根据茎叶图，比较两城市满意度评分的平均值的大小及方差的大小（不要求计算出具体值，给出结论即可）；

    （2）若得分不低于80分，则认为该用户对此种交通方式“认可”，否则认为该用户对此种交通方式“不认可”，请根据此样本完成此2×2列联表，并据此样本分析是否有95%的把握认为城市拥堵与认可共享单车有关；

    A

    B

    合计

    认可

    不认可

    合计

    （3）在A，B城市对此种交通方式“认可”的用户中按照分层抽样的方法抽取6人，若在此6人中推荐2人参加“单车维护”志愿活动，求A城市中至少有1人的概率。

    参考数据如下：（下面临界值表供参考）

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    （参考公式，其中）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】足球是当今世界传播范围最广、参与人数最多的体育运动，具有广泛的社会影响，深受世界各国民众喜爱．

    （1）为调查大学生喜欢足球是否与性别有关，随机选取50名大学生进行问卷调查，当问卷评分不低于80分则认为喜欢足球，当评分低于80分则认为不喜欢足球，这50名大学生问卷评分的结果用茎叶图表示如图：

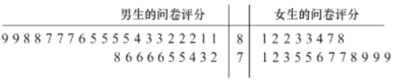
    请依据上述数据填写如下列联表：

    喜欢足球

    不喜欢足球

    总计

    女生

    男生

    总计

    请问是否有 的把握认为喜欢足球与性别有关？

    参考公式及数据：，．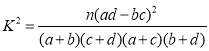

    0.100

    0.050

    0.010

    0.001

    2.706

    3.841

    6.635

    10.828

    （2）已知某国“糖果盒”足球场每年平均上座率与该国成年男子国家足球队在国际足联的年度排名线性相关，数据如表，，，

    年度排名

    9

    6

    3

    平均上座率

    0.9

    0.91

    0.92

    0.93

    0.95

    求变量与的线性回归方程，并预测排名为1时该球场的上座率．

    参考公式及数据：，；．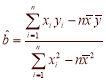

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为（为参数）.在以坐标原点为极点，轴正半轴为极轴的极坐标系中，曲线的极坐标方程为.

    （1）写出的普通方程和的直角坐标方程；

    （2）若与相交于两点，求的面积.

    查看答案和解析>>

    同步练习册答案