
【题目】已知以点A(m, ![]() )(m∈R且m>0)为圆心的圆与x轴相交于O,B两点,与y轴相交于O,C两点,其中O为坐标原点.
)(m∈R且m>0)为圆心的圆与x轴相交于O,B两点,与y轴相交于O,C两点,其中O为坐标原点.
(1)当m=2时,求圆A的标准方程;
(2)当m变化时,△OBC的面积是否为定值?若是,请求出该定值;若不是,请说明理由;
(3)设直线![]() 与圆A相交于P,Q两点,且 |OP|=|OQ|,求 |PQ| 的值.
与圆A相交于P,Q两点,且 |OP|=|OQ|,求 |PQ| 的值.
【答案】(1)![]() ;(2)
;(2)![]() 的面积为定值;(3)
的面积为定值;(3) ![]()
【解析】
试题(1)由![]() 可求得圆心坐标,由
可求得圆心坐标,由![]() 的值可求得圆的半径,进而得到圆的方程;(2)由圆的方程可求得
的值可求得圆的半径,进而得到圆的方程;(2)由圆的方程可求得![]() 两点坐标,将面积转化为用两点坐标表示,可得其为定值;(3)由|OP|=|OQ|可得点O在线段PQ的垂直平分线上,结合圆心也在线段PQ的垂直平分线上,从而可得
两点坐标,将面积转化为用两点坐标表示,可得其为定值;(3)由|OP|=|OQ|可得点O在线段PQ的垂直平分线上,结合圆心也在线段PQ的垂直平分线上,从而可得![]() ,由此可求得
,由此可求得![]() 的值,即求得圆心坐标,结合直线与圆相交的弦长问题可求得
的值,即求得圆心坐标,结合直线与圆相交的弦长问题可求得![]() 的值.
的值.
(1)当![]() 时,圆心
时,圆心![]() 的坐标为
的坐标为![]() ,
,
∵圆![]() 过原点
过原点![]() , ∴
, ∴![]() ,
,
则圆![]() 的方程是
的方程是![]() ;
;
(2)∵圆![]() 过原点
过原点![]() , ∴
, ∴![]() =
=![]() ,
,
则圆![]() 的方程是
的方程是![]() ,
,
令![]() ,得
,得![]() ,∴
,∴![]() ;
;
令![]() ,得
,得![]() ,∴
,∴![]() ,
,
∴![]() , 即:
, 即:![]() 的面积为定值;
的面积为定值;
(3)∵![]() , ∴
, ∴![]() 垂直平分线段
垂直平分线段![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,解得
,解得![]() .
.
∵ 已知![]() ,∴
,∴![]() ,
,
∴ 圆![]() 的方程为
的方程为![]() .
.
![]() ,
,
![]() 此圆
此圆![]() 与直线
与直线![]() 相交于两点,
相交于两点,
![]() .
.


科目:高中数学 来源: 题型:
【题目】已知直线![]() 的方程为
的方程为![]() ,抛物线
,抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,点
,点![]() 是抛物线
是抛物线![]() 上到直线
上到直线![]() 距离最小的点.
距离最小的点.
(1)求点![]() 的坐标;
的坐标;
(2)若直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,
两点,![]() 为
为![]() 中点,且
中点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,上顶点为
,上顶点为![]() ,若直线
,若直线![]() 的斜率为1,且与椭圆的另一个交点为
的斜率为1,且与椭圆的另一个交点为![]() ,
, ![]() 的周长为
的周长为![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 的直线
的直线![]() (直线
(直线![]() 的斜率不为1)与椭圆交于
的斜率不为1)与椭圆交于![]() 两点,点
两点,点![]() 在点
在点![]() 的上方,若
的上方,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为进一步贯彻落实“十九”大精神,某高校组织了“歌颂祖国,紧跟党走”为主题的党史知识竞赛,从参加竞赛的学生中,随机抽取40名学生,将其成绩分为六段![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
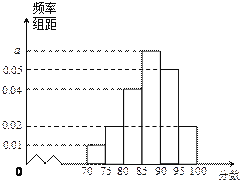
(1)求图中![]() 的值;
的值;
(2)若从竞赛成绩在![]() 与
与![]() 两个分数段的学生
两个分数段的学生![]() 中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于
中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于![]() 分为事件
分为事件![]() ,求事件发生的概率.
,求事件发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】20名学生某次数学考试成绩(单位:分)的频率分布直方图如下:

(1)求频率直方图中a的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(3)从成绩在[50,70)的学生中人选2人,求这2人的成绩都在[60,70)中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com