
【题目】(本小题满分为14分)已知定义域为R的函数![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
【答案】(1)a=2,b=1.(2)![]()
【解析】试题分析:(1)由函数是奇函数可得![]() ,将
,将![]() 代入两个特殊值得到关于
代入两个特殊值得到关于![]() 的方程组求解其值;(2)首先利用定义法判断函数的单调性,利用奇函数将不等式变形为f(x2-x)< f(-2x2+t),,利用单调性得到关于
的方程组求解其值;(2)首先利用定义法判断函数的单调性,利用奇函数将不等式变形为f(x2-x)< f(-2x2+t),,利用单调性得到关于![]() 的恒成立不等式,分离参数
的恒成立不等式,分离参数![]() 后通过求函数最值得到
后通过求函数最值得到![]() 的取值范围
的取值范围
试题解析:(1)∵f(x)是奇函数且0∈R,∴f(0)=0即![]()
∴![]()
又由f(1)=-f(-1)知
![]() a=2
a=2
∴f(x)=![]()
(2)证明设x1,x2∈(-∞,+∞)且x1<x2
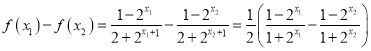
![]() ·
·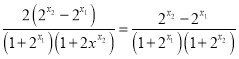
∵y=2x在(-∞,+∞)上为增函数且x1<x2,∴![]()
且y=2x>0恒成立,∴![]()
∴f(x1)-f(x2)>0 即f(x1)>f(x2)
∴f(x)在(-∞,+∞)上为减函数
∵f(x)是奇函数f(x2-x)+f(2x2-t)<0等价于f(x2-x)<-f(2x2-t)=f(-2x2+t)
又∵f(x)是减函数,∴x2-x>-2x2+t
即一切x∈R,3x2-x-t>0恒成立
∴△=1+12t<0,即t<![]()


科目:高中数学 来源: 题型:
【题目】近几年来,我国许多地区经常出现干旱现象,为抗旱经常要进行人工降雨,现由天气预报得知,某地在未来5天的指定时间的降雨概率是:前3天均为![]() ,后2天均为
,后2天均为![]() ,5天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.
,5天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.
(1)求至少有1天需要人工降雨的概率;
(2)求不需要人工降雨的天数![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为![]() ,如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组
,如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组![]() 的人数为4人.
的人数为4人.
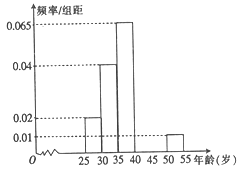
(1)求第五组的频率并估计200名志愿者中年龄在40岁以上(含40岁)的人数;
(2)若从年龄位于第四组和第六组的志愿者中随机抽取两名,记他们的年龄分别为![]() ,事件
,事件![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
, ![]() (
(![]() ).
).
(Ⅰ)求函数![]() 的单调增区间;
的单调增区间;
(Ⅱ)当![]() 时,记
时,记![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人玩数字游戏,先由甲任想一个数字记为a,再由乙猜甲刚才想的数字,把乙想的数字记为b,且a,b∈{1,2,3,4,5,6},记ξ=|a﹣b|.
(1)求ξ=1的概率;
(2)若ξ≤1,则称“甲乙心有灵犀”,求“甲乙心有灵犀”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式x2≤5x﹣4的解集为A.
(1)求集合A;
(2)设关于x的不等式x2﹣(a+2)x+2a≤0的解集为M,若MA,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】简阳羊肉汤已入选成都市级非遗项目,成为简阳的名片。当初向各地作了广告推广,同时广告对销售收益也有影响。在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
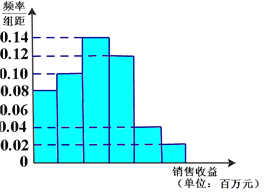
(Ⅰ)根据频率分布直方图,计算图中各小长方形的宽度;
(Ⅱ)根据频率分布直方图,估计投入4万元广告费用之后,并将各地销售收益的平均值(以各组的区间中点值代表该组的取值);
(Ⅲ)按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
销售收益y(单位:百万元) | 2 | 3 | 2 | 7 |
表中的数据显示,![]() 与
与![]() 之间存在线性相关关系,请将(Ⅱ)的结果填入空白栏,并计算
之间存在线性相关关系,请将(Ⅱ)的结果填入空白栏,并计算![]() 关于
关于![]() 的回归方程.回归直线的斜率和截距的最小二乘估计公式分别为
的回归方程.回归直线的斜率和截距的最小二乘估计公式分别为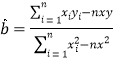 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax+1|+|2x﹣1|(a∈R).
(1)当a=1时,求不等式f(x)≥2的解集;
(2)若f(x)≤2x在x∈[![]() ,1]时恒成立,求a的取值范围.
,1]时恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com