
【题目】《九章算术》卷五《商功》中有如下叙述“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈“刍甍”指的是底面为矩形的对称型屋脊状的几何体,“下广三丈”是指底面矩形宽三丈,“袤四丈”是指底面矩形长四丈,“上袤二丈”是指脊长二丈,“无宽”是指脊无宽度,“高一丈”是指几何体的高为一丈.现有一个刍甍如图所示,下广三丈,袤四丈,上袤三丈,无广,高二丈,则该刍甍的外接球的表面积为_______________平方丈.

 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
【题目】第七届世界军人运动会(7th CISM Military World Games) ,简称"武汉军运会”,于2019年10月18日至27日在中国武汉举行,共设置射击、游泳、田径篮球等27个大项、329个小项.来自100多个国家的近万名现役军人同台竞技.会议期间,某公司欲采购海南某水果种植基地的水果,公司王总经理与该种植基地的负责人张老板商定一次性采购一种水果的采购价![]() (千元/吨)与采购量
(千元/吨)与采购量![]() (吨)之间的函数关系的图象如图中的折线
(吨)之间的函数关系的图象如图中的折线![]() 所示(不包含端点
所示(不包含端点![]() ,但包含端点
,但包含端点![]() ).
).

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)已知该水果种植基地种植该水果的成本是8千元/吨,那么王总经理的采购量为多少时,该水果基地在这次买卖中所获得利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 且
且![]() .
.
(1)若函数![]() 在
在![]() 上恒有意义,求
上恒有意义,求![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 上为增函数,且最大值为
上为增函数,且最大值为![]() ?若存在求出
?若存在求出![]() 的值,若不存在请说明理由.
的值,若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
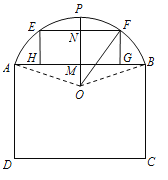
【题目】下图为某仓库一侧墙面的示意图,其下部是矩形ABCD,上部是圆弧AB,该圆弧所在的圆心为O,为了调节仓库内的湿度和温度,现要在墙面上开一个矩形的通风窗EFGH(其中E,F在圆弧AB上,G,H在弦AB上).过O作![]() ,交AB 于M,交EF于N,交圆弧AB于P,已知
,交AB 于M,交EF于N,交圆弧AB于P,已知![]() (单位:m),记通风窗EFGH的面积为S(单位:
(单位:m),记通风窗EFGH的面积为S(单位:![]() )
)
(1)按下列要求建立函数关系式:
(i)设![]() ,将S表示成
,将S表示成![]() 的函数;
的函数;
(ii)设![]() ,将S表示成
,将S表示成![]() 的函数;
的函数;
(2)试问通风窗的高度MN为多少时,通风窗EFGH的面积S最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中x>0,k为常数,e为自然对数的底数.
,其中x>0,k为常数,e为自然对数的底数.
(1)当k≤0时,求![]() 的单调区间;
的单调区间;
(2)若函数![]() 在区间(1,3)上存在两个极值点,求实数k的取值范围;
在区间(1,3)上存在两个极值点,求实数k的取值范围;
(3)证明:对任意给定的实数k,存在![]() (
(![]() ),使得
),使得![]() 在区间(
在区间(![]() ,
,![]() )上单调递增.
)上单调递增.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com