
(1)求相邻两面所成二面角的大小;
(2)求相邻两面中心的距离;
(3)求两个相对面之间的距离.
解:(1)如图所示,分别取BE,CD的中点M,N,连结AM,AN,FM,FN,MN.
因为△ACD,△FCD均为全等的正三角形,
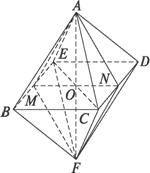
所以AN=NF=FM=MA.
故四边形AMFN为菱形,且CD⊥AN,CD⊥FN,故∠ANF是正八面体相邻两面所成二面角的平面角.
在菱形AMFN中,边长为![]() a.
a.
在正方形BCDE中,边长为a,连结CE并设CE∩MN=O,则
AO=![]() .
.
所以AF=2AO=![]() a,
a,
cos∠ANF=![]() .
.
所以∠ANF=π-arccos![]() .
.
(2)分别在AN,FN上取一点G1,G2,使NG1=![]() AN,NG2=
AN,NG2=![]() FN,则G1,G2分别是正三角形ACD和FCD的中心,连结G1G2.
FN,则G1,G2分别是正三角形ACD和FCD的中心,连结G1G2.
则G1G2∥AF,故![]() =
=![]() ,得G1G2=
,得G1G2=![]() a.
a.
(3)正八面体两相对面之间的距离就是菱形对边之间的距离.在菱形AMFN中,设AN与MF之间的距离为d,则MF·d=![]() MF·AF.
MF·AF.
而MF=![]() a,MN=a,AF=
a,MN=a,AF=![]() a,
a,
由此可得d=![]() a.
a.


科目:高中数学 来源: 题型:
| 2 |
| 2 |
| A、圆 | B、抛物线 | C、双曲线 | D、椭圆 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com