
【题目】已知函数f(x)=f'(1)ex﹣1﹣f(0)x+ ![]() 的导数,e为自然对数的底数)g(x)=
的导数,e为自然对数的底数)g(x)= ![]() +ax+b(a∈R,b∈R)
+ax+b(a∈R,b∈R)
(Ⅰ)求f(x)的解析式及极值;
(Ⅱ)若f(x)≥g(x),求 ![]() 的最大值.
的最大值.
【答案】解:(Ⅰ)由已知得:f′(x)=f′(1)ex﹣1﹣f(0)+x,令x=1,得:f′(1)=f′(1)﹣f(0)+1,
即f(0)=1,
∵f(0)= ![]() ,
,
∴f′(1)=e,
从而f(x)=ex﹣x+ ![]() x2 ,
x2 ,
∴f′(x)=ex+x﹣1,
又f′(x)=ex+x﹣1在R递增,且f′(0)=0,
∴当x<0时,f′(x)<0,x>0时,f′(x)>0,
故x=0为极值点,
∴f(0)= ![]() ;
;
(Ⅱ)f(x)≥ ![]() x2+ax+bh(x)=ex﹣(a+1)x﹣b≥0,
x2+ax+bh(x)=ex﹣(a+1)x﹣b≥0,
得:h′(x)=ex﹣(a+1),
①当a+1≤0时,h′(x)>0,
故y=h(x)在x∈R上递增,
x∈﹣∞时,h(x)→﹣∞与h(x)≥0矛盾,
②当a+1>0时,h′(x)>0,
∴x>ln(a+1),h′(x)<0,
∴x<ln(a+1),
故x=ln(a+1)时,h(x)min=(a+1)﹣(a+1)ln(a+1)﹣b≥0,
即(a+1)﹣(a+1)ln(a+1)≥b,
∴(a+1)b≤(a+1)2﹣(a+1)2ln(a+1),(a+1>0),
令F(x)=x3﹣x2lnx(x>0),则F′(x)=x(1﹣2lnx),
∴F′(x)>0,解得:0<x< ![]() ,F′(x)<0,解得:x>
,F′(x)<0,解得:x> ![]() ,
,
x= ![]() 时,F(x)max=
时,F(x)max= ![]() ,
,
即当a= ![]() ﹣1,b=
﹣1,b= ![]() 时,
时,
(a+1)b的最大值为 ![]() ,
,
∴ ![]() 的最大值为:
的最大值为: ![]()
【解析】(Ⅰ)求出函数的导数,求出f′(1)=e,求出函数的导数,得到函数的单调性求出f(0)的值即可;(Ⅱ)令h(x)=ex﹣(a+1)x﹣b≥0,求出函数的导数,通过讨论a的范围,求出函数的单调区间,求出 ![]() 的最大值即可.
的最大值即可.
【考点精析】通过灵活运用基本求导法则和函数的极值与导数,掌握若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧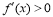 ,那么
,那么![]() 是极小值即可以解答此题.
是极小值即可以解答此题.


科目:高中数学 来源: 题型:
【题目】下列四个命题中,正确的个数是( )
①命题“存在x∈R,x2﹣x>0”的否定是“对于任意的x∈R,x2﹣x<0”;
②若函数f(x)在(2016,2017)上有零点,则f(2016)f(2017)<0;
③在公差为d的等差数列{an}中,a1=2,a1 , a3 , a4成等比数列,则公差d为﹣ ![]() ;
;
④函数y=sin2x+cos2x在[0, ![]() ]上的单调递增区间为[0,
]上的单调递增区间为[0, ![]() ].
].
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 分别是椭圆
分别是椭圆 ![]() 的左、右焦点,离心率为
的左、右焦点,离心率为 ![]() ,
, ![]() ,
, ![]() 分别是椭圆的上、下顶点,
分别是椭圆的上、下顶点, ![]() .
.
(Ⅰ)求椭圆 ![]() 的方程;
的方程;
(Ⅱ)过 ![]() (0,2)作直线
(0,2)作直线 ![]() 与
与 ![]() 交于
交于 ![]() 两点,求三角形
两点,求三角形 ![]() 面积的最大值(
面积的最大值( ![]() 是坐标原点).
是坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin2x+sinxcosx﹣
sin2x+sinxcosx﹣ ![]()
(1)求函数y=f(x)在[0, ![]() ]上的单调递增区间;
]上的单调递增区间;
(2)将函数y=f(x)的图象向左平移 ![]() 个单位长度,再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,求证:存在无穷多个互不相同的整数x0 , 使得g(x0)>
个单位长度,再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=g(x)的图象,求证:存在无穷多个互不相同的整数x0 , 使得g(x0)> ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f'(x)是函数f(x)的导数,f'(x)是函数f'(x)的导数,若方程f'(x)=0有实数解x0 , 则称点(x0 , f(x0))为函数f(x)的拐点.某同学经过探究发现:任何一个三次函数f(x)=ax3+bx2+cx+d(a≠0)都有拐点,任何一个三次函数都有对称中心,且拐点就是对称中心,
设函数g(x)=x3﹣3x2+4x+2,利用上述探究结果
计算: ![]() =
=
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a,b是不相等的两个正数,且blna﹣alnb=a﹣b,给出下列结论:①a+b﹣ab>1;②a+b>2;③ ![]() +
+ ![]() >2.其中所有正确结论的序号是( )
>2.其中所有正确结论的序号是( )
A.①②
B.①③
C.②③
D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的方程为y=x+2,点P是抛物线y2=4x上到直线l距离最小的点,点A是抛物线上异于点P的点,直线AP与直线l交于点Q,过点Q与x轴平行的直线与抛物线y2=4x交于点B.
(Ⅰ)求点P的坐标;
(Ⅱ)证明直线AB恒过定点,并求这个定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上海市松江区天马山上的“护珠塔”因其倾斜度超过意大利的比萨斜塔而号称“世界第一斜塔”.兴趣小组同学实施如下方案来测量塔的倾斜度和塔高:如图,记O点为塔基、P点为塔尖、点P在地面上的射影为点H.在塔身OP射影所在直线上选点A,使仰角k∠HAP=45°,过O点与OA成120°的地面上选B点,使仰角∠HPB=45°(点A,B,O都在同一水平面上),此时测得∠OAB=27°,A与B之间距离为33.6米.试求: 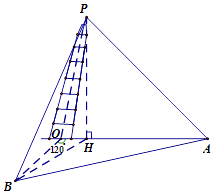
(1)塔高(即线段PH的长,精确到0.1米);
(2)塔身的倾斜度(即PO与PH的夹角,精确到0.1°).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·上海)设z1, z2![]() C, ,则“z1, z2中至少有一个数是虚数”是“z1-z2是虚数”的( )
C, ,则“z1, z2中至少有一个数是虚数”是“z1-z2是虚数”的( )
A.充分非必要条件
B.必要非充分条件
C.充要条件
D.既非充分又非必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com